1、填空题  带电体周围存在着电场，而______力和库仑力有类似的规律，不妨认为有质量的物体周围存在着引力场，那么在地球周围就存在着重力场，我们可以用定义电场强度的方法来定义重力场强度，由此可得重力场强度为______．

参考答案：电场强度的定义式为E=Fq，其中q为放入电场中的检验电荷，F为其受到的电场力．类似的，我们在质量为M的质点相距r处放入一个检验质点，其质量为m，则其受到的万有引力F=GMmr2=mg 与其质量m之比GMr2或g，与检验质点无关，只由场源质量M、到场源距离r决定，我们定义它为引力场强度EG=Fm=GMr2=g．
故答案为：万有引力，g．

本题解析：

本题难度：简单

2、选择题  下列说法不正确的是? (? )
A．牛顿运动定律只适用于低速运动的宏观物体
B．牛顿从实验研究中发现了万有引力定律并精确测定了引力常数
C．卡文迪许利用扭秤装置首次测出了万有引力常量，从而“秤出了”地球的质量
D．伽利略科学思想方法的核心是实验与逻辑推理和谐结合

参考答案：B

本题解析：本题考查物理学史。牛顿运动定律经典力学只适用于低速运动的宏观物体，A正确；牛顿发现了万有引力定律，卡文迪许测出了万有引力常量，B错误C正确；伽利略科学思想方法的核心是实验与逻辑推理和谐结合，D正确；选B。

本题难度：简单

3、选择题  假定地球、月球都静止不动，用火箭从地球沿地月连线发射一探测器．假定探测器在地球表面附近脱离火箭．用W表示探测器从脱离火箭处飞到月球的过程中克服地球引力做的功，用Ek表示探测器脱离火箭时的动能，若不计空气阻力，则（　　）
A．Ek必须大于或等于W，探测器才能到达月球
B．Ek小于W，探测器也可能到达月球
C．Ek=

参考答案：探测器脱离火箭后同时受到地球的引力和月球的引力，
根据F=GMmr2
可知开始时物体受到地球的引力大于受到月球的引力，后来受到月球的引力大于受到地球的引力，
所以探测器在运动的过程中地球的引力对物体做负功，月球的引力对物体做正功，
所以探测器能够到达月球的条件是必须克服地球引力做功越过引力相等的位置．
又根据F=GMmr2可知探测器受到的引力相等的位置的位置距离地球远而距离月球近，
设在探测器运动的过程中月球引力对探测器做的功为W1，探测器克服地球引力对探测器做的功为W，并且W1＜W，
若探测器恰好到达月球，则根据动能定理可得
-W+W1=EK末-Ek，
即EK末=EK-W+W1
故探测器能够到达月球的条件是Ek末=EK-W+W1≥0，
即EK≥W-W1，
故EK小于W时探测器也可能到达月球．
故B正确．
由于M地≈81M月，
故W≈81W1
假设当EK=12W时探测器能够到达月球，则Ek≥W-W1仍然成立，可转化为12W≥W-W1仍然成立，即应有W1≥12W，这显然与W≈81W1
相矛盾，故假设不正确．即探测器一定不能到达月球．
故D正确．
故选B、D．

本题解析：

本题难度：简单

4、简答题  
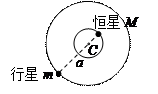
（1）试在图中粗略画出恒星运动的轨道和位置；
（2）试计算恒星与点C间的距离和恒星的运行速率v．

参考答案：
（1）

（2）

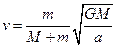
本题解析：(1)恒星运动的轨道和位置大致如图． (圆和恒星位置各2分)

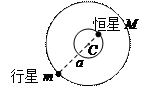
(2)对行星m?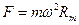?①（2分）
对恒星M?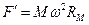?②（2分）?
根据牛顿第三定律，F与F′大小相等
由①②得??③（2分）
对恒星M?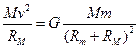?④（2分）
代入数据得?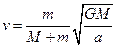?⑤?（2分）

本题难度：简单

5、选择题  如图，在月球附近圆轨道上运行的“嫦娥二号”，到A点时变为椭圆轨道，B点是近月点，则

A．从A点运动到B点过程中，“嫦娥二号”受到月球的引力增大
B．从A点运动到B点过程中，月球对“嫦娥二号”的引力做负功
C．“嫦娥二号”在Ａ点比在Ｂ点的速度小
D．“嫦娥二号”在Ａ点比在Ｂ点的速度大

参考答案：AC

本题解析：嫦娥二号运行过程中，万有引力充当向心力，从A点运动到B点过程中，运行半径减小，所以根据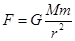可得嫦娥二号受到月球的引力增大，A正确，从A点运动到B点过程中，沿引力方向运动，所以引力做正功，速度增大，BD错误,C正确；本题也可以通过公式，线速度大小与半径成反比，来判断速度的变化

本题难度：一般