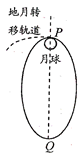
1、选择题  探月卫星沿地月转移轨道到达月球附近，在P点进行第一次“刹车制动”后被月球捕获，进入椭圆轨道绕月飞行，如图所示。若卫星的质量为m，远月点Q距月球表面的高度为h，运行到Q点时它的角速度为w，加速度为a，月球的质量为M、半径为R，月球表面的重力加速度为g，引力常量为G，则卫星在远月点Q时对月球的万有引力大小为

A．ma
B．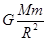
C．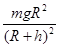
D．m（R+h)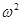

参考答案：AC

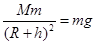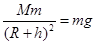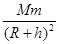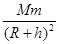本题解析：卫星在远月点时月球的万有引力为F=G?，故B错误，A正确：又在月球表面有：G得GM=R2g代入F=G，得F=故? C正确；又卫星绕月球沿椭圆轨道运行，故D错误。

本题难度：简单

2、选择题  多选
组成星球的物质是靠引力吸引在一起的，这样的星球有一个最大的自转速率，如果超过了该速率，星球的万有引力将不足以维持其赤道附近的物体做圆周运动，由此能得到半径为r，密度为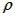，质量为M且均匀分布的星球的最小自转周期T，下列表达式中正确的是（万有引力常量为G）（ ? ）
A．
B．
C．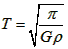
D．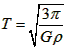

参考答案：AD

本题解析：

本题难度：一般

3、计算题  两颗星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动．现测得两颗星中心距离为R ，其运动周期为T，求两颗星的总质量．

参考答案：解：
设两颗星质量分别为M1 和M2 ，都绕连线上的O 点做周期为T 的圆周运动，星球1 和星球2 到O 点的距离分别为l1 和l2 ，由万有引力定律和牛顿第二定律及几何条件可得
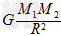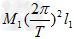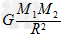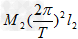=，=，l1+l2=R．
联立解得M1+M2=．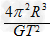

本题解析：

本题难度：一般

4、选择题  两颗靠得较近的天体叫双星，它们以两者重心连线上的某点为圆心做匀速圆周运动，因而不至于因引力作用而吸引在一起，以下关于双星的说法中正确的是 （?）
A．它们做圆周运动的角速度与其质量成反比
B．它们做圆周运动的线速度与其质量成反比
C．它们所受向心力与其质量成反比
D．它们做圆周运动的半径与其质量成反比

参考答案：D

本题解析：根据题意的双星的示意图

双星系统提供彼此的万有引力，即，其中L指的是两星之间的距离，r1，r2指的是各星的圆周半径。因此根据上式可得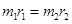它们做圆周运动的半径与其质量成反比，D正确
点评：本题考查了利用万有引力研究双星系统，在双星系统中，只要是彼此万有引力相同，从而建立等式求解。

本题难度：简单

5、选择题  2008年9月25日，“神舟七号”顺利升空入轨，入轨一段时间后需要进行轨道维持，所谓“轨道维持”就是通过控制飞船上发动机的点火时间、推力的大小和方向，使飞船能保持在预定轨道上稳定运行．如果不进行轨道维持，由于飞船受轨道上稀薄空气的摩擦阻力，轨道高度会逐渐缓慢降低，在这种情况下，下列说法中正确的是（　　）
A．飞船受到的万有引力逐渐增大，线速度逐渐减小
B．飞船的向心加速度逐渐增大，周期逐渐减小
C．飞船的动能、重力势能和机械能都逐渐减小
D．重力势能逐渐减小，动能逐渐增大，机械能逐渐减小

参考答案：A、由万有引力提供向心力可得：F=GMmr2=mv2r，由于轨道半径减小，故可知万有引力增大，线速度v=

本题解析：

本题难度：一般