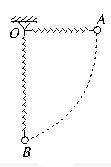
1、选择题  如图所示，一轻弹簧固定于O点，另一端系一重物，将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放，让它自由摆下，不计空气阻力，在重物由A点摆向最低点的过程中

A.重物的重力势能减少
B.重物的重力势能增大
C.重物的机械能不变
D.重物的机械能减少

参考答案：AD

本题解析：物体从A点释放后，在从A点向B点运动的过程中，物体的重力势能逐渐减小，动能逐渐增加，弹簧逐渐被拉长，弹性势能逐渐增大，所以，物体减小的重力势能一部分转化为物体的动能，另一部分转化为弹簧的弹性势能.对物体和弹簧构成的系统，机械能守恒，但对物体来说，其机械能减小.选项A、D正确

本题难度：简单

2、填空题  （A）一辆电动自行车铭牌上的技术参数如下表所示：

参考答案：（1）电车以最大速度匀速运动时，受力平衡，有
F=f=0.02mg=0.02×（30+70）×10=20N
P出=Fvm
解得
vm=P出f=12020=6m/s
即人骑车行驶的最大速度为6m/s；
（2）当车速为v1=3.0m/s时，根据牛顿第二定律，有
P出v1-f=ma
解得
a=0.2m/s2
即仅在直流电机提供动力的情况下，当车速为v1=3.0m/s时，人骑车的最大加速度为0.2m/s2．
故答案为：6，0.2．

本题解析：

本题难度：简单

3、填空题  质量为m的跳水运动员从距水面H高处跳下，落入水中后受到水的阻力而做减速运动。设水对他的阻力大小恒为F，运动员从离开跳台到落入水中减速下降h高度的过程中，他的重力势能减少了?，他的机械能减少了?。

参考答案：mg（H+h）；Fh

本题解析：机械能守恒定律应用专题．功是能量转化的量度，重力势能的减小量等于重力做的功，机械能的变化量等于除重力外其余力做的功．
重力势能的减小量等于重力做的功，运动员下降过程，重力做的总功为mg（H+h），故重力势能减小mg（H+h）；
运动员下降过程中，除重力外，克服阻力做功为FH，故机械能减小Fh；．

本题难度：简单

4、简答题  如图，长木板ab的b端固定一挡板，木板连同挡板的质量为M=4.0kg，a、b间距离s=2.0m．木板位于光滑水平面上．在木板a端有一小物块，其质量m=1.0kg，小物块与木板间的动摩擦因数μ=0.10，它们都处于静止状态．现令小物块以初速v0=4.0m/s，沿木板向前滑动，直到和挡板相碰．碰撞后，小物块恰好回到a端而不脱离木板．求碰撞过程中损失的机械能．

参考答案：设木板和物块最后共同运动的速度为v，由动量守恒定律mv0=（m+M）v-----①
设全过程损失的机械能为E，E=12mv20-12(m+M)v2------------②
用W表示在全过程中摩擦力做的总功，则W=-2μmgs----------③
用E1表示在碰撞过程中损失的机械能，则E1=E-W-------④
由以上各式解得E=12mMm+mv20-2μmgs-----------⑤
代入数据解锝
E1=2.4J?
碰撞过程中损失的机械能为2.4J．

本题解析：

本题难度：一般

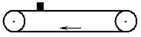
5、选择题  如图，水平传送带保持 1 m/s 的速度运动．一质量为1 kg的物体与传送带间的动摩擦因数为0.2，现将该物体无初速地放到传送带上，则物体在运动1m的过程中，皮带对该物体做的功为（g ="10" m/s2）

A．0.5J
B．2J
C．2.5J
D．5J

参考答案：A

本题解析：
本题考查动能定理的应用；匀变速直线运动的位移与时间的关系；牛顿第二定律。解答本题关键是首先要分析物体的运动过程，判断物块是否一直做匀加速运动。
物体无初速地放到传送带上，开始阶段受到滑动摩擦力而做匀加速运动，匀加速运动的过程中加速度为?。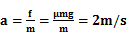
设物块从放上皮带到速度与皮带相同经历的时间为t，则有
?
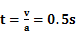通过的位移为?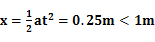
所以速度与皮带相同后，物块做匀速直线运动。只有匀加速运动过程，皮带对物块做功。根据动能定理得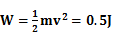　
故选A

本题难度：简单