1、选择题  质量为m的小球，以速度v在高为H的光滑平台上运动，当它滑离平台下落经过高为h的某一点（以地面为零势能面），它的（?）
A．重力势能为mg（H—h）
B．动能为mgh+mv2/2；
C．动能的增加量为mg（H—h）
D．机械能为mgH+ mv2/2

参考答案：CD

本题解析：由于物体距离地面高度为h，重力势能为mgh，选项A错误；由动能定理，可知末动能为mg（H-h）+mv2/2，选项B错误；同理判断CD正确；故选CD
点评：本题难度较小，重力势能的大小与零势能面的选取有关，本题中机械能大小可根据机械能守恒判断和计算

本题难度：简单

2、填空题  如图所示，劲度系数为k2的轻弹簧竖直放在桌面上（与桌面不粘连），上端固连一质量为m的物块．另一劲度系数为k1的轻弹簧下端固连在物块上．现将k1的上端A缓慢上提，当k2的弹力大小等于

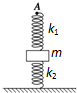
参考答案：对末态时的物块受力分析，受重力、弹簧K1的向上的拉力F1′与弹簧K2的向上的弹力F2′，物块静止有
F1′+F2′=mg
初态时，弹簧k2（压缩）的弹力F2=mg
末态时，弹簧k2（压缩）的弹力F2′=23mg
弹簧k2的长度变化量△x2=mg3k2
重力势能增加量△EP=mg△x2=(mg)23k2
由F1′+F2′=mg，F2′=23mg
得：F1′=13mg
初态时，弹簧k1（原长）的弹力F1=0
末态时，弹簧k1（伸长）的弹力F1′=13mg
弹簧k1的长度变化量△x1=△F1K1=mg3k1
由几何关系知所求距离为△x1+△x2=13mg(1k1+1k2)
故答案为：(mg)23k2，13mg(1k1+1k2)

本题解析：

本题难度：一般

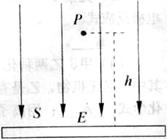
3、选择题  如图所示，空间有竖直向下的匀强电场，电场强度为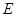，在电场中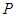处由静止下落一质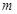量为、带电量为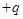的小球(可视为质点)。在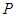的正下方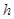处有一水平弹性绝缘挡板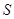(挡板不影响电场的分布)，小球每次与挡板相碰后电量减小到碰前的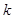倍(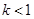)，而碰撞过程中小球的机械能不损失，即碰撞前后小球的速度大小不变，方向相反。设在匀强电场中，挡板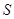处的电势为零，则下列说法正确的是

A．小球在初始位置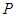处的电势能为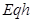
B．小球第一次与挡板相碰后所能达到的最大高度大于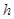
C．小球第一次与挡板相碰后返回P点速度为0
D．小球第一次与挡板相碰后所能达到最大高度时的电势能小于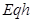

参考答案：ABD

本题解析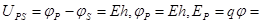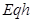：，A对；第一次碰撞后小球的电荷量减小，由电场力做功W=qU可判断出小球上升到P点上方，B对；C错；小球碰撞前，碰撞后上升到最高点，有两个式子可判断D对；

本题难度：简单

4、选择题  如上图所示，足够长且电阻不计的光滑平行金属导轨MN、PQ竖直放置，间距为L=0.5m，一匀强磁场B=0.2T垂直穿过导轨平面，导轨的上端M与P间连接阻值为R＝0.40Ω的电阻，质量为m＝0.01kg、 电阻不计的金属棒ab垂直紧贴在导轨上．现使金属棒ab由静止开始下滑，经过一段时间金属棒达到稳定状态,这段时间内通过R的电量0.3C，则在这一过程中（?）(g=10m/s2 ）

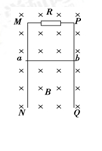
A．安培力最大值为0.05N，
B．这段时间内下降的高度1.2m
C．重力最大功率为0.1w
D．电阻产生的焦耳热为0.04J

参考答案：BD

本题解析：
试题分析:安培力的最大值应该等于重力0.1N，故A错误；由法拉第电磁感应定律和闭合电路欧姆定律可知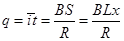，解得x=1.2m，故B正确；当安培力等于重力时，速度最大，，解得，重力最大功率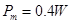，故C错误；由能量守恒定律，电阻产生的焦耳热，故D正确。

本题难度：一般

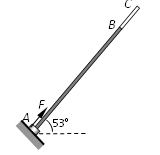
5、计算题   如图，一根直杆由粗细相同的两段构成，其中AB段为长x1=5m的粗糙杆，BC段为长x2=1m的光滑杆。将杆与水平面成53°角固定在一块弹性挡板上，在杆上套一质量m=0.5kg、孔径略大于杆直径的圆环。开始时，圆环静止在杆底端A。现用沿杆向上的恒力F拉圆环，当圆环运动到B点时撤去F，圆环刚好能到达顶端C，然后再沿杆下滑。已知圆环与AB段的动摩擦因数μ=0.1，g=10m/s2，sin53°=0.8，cos53°=0.6。试求：

小题1:拉力F的大小；
小题2:拉力F作用的时间；
小题3:若不计圆环与挡板碰撞时机械能损失，从圆环开始运动到最终静止的过程中在粗糙杆上所通过的总路程。

参考答案：
小题1:5.1N
小题2:
小题3: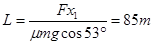

本题解析：（1）AC过程：根据动能定理?有
?（3分）
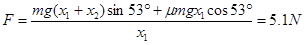恒力?（2分）
（2）AB过程：根据牛顿第二定律和运动学公式?有
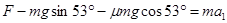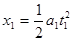?（2分）
???（2分）
解得 加速度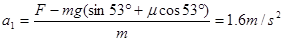
时间?（1分）
（3）从圆环开始运动到最终静止在粗糙杆上通过的总路程为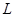
根据动能定理?有??（3分）
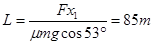总路程?（2分）
解法（二）
（1）AB过程：根据牛顿第二定律和运动学公式?有
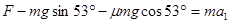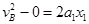?（1分）
?（1分）
BC过程：根据牛顿第二定律和运动学公式?有
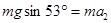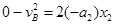?（1分）
?（1分）
联立解得?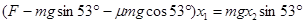
恒力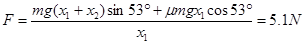?（1分）
（2）BC过程：根据牛顿第二定律和运动学公式?有
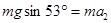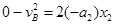?（1分）
?（1分）
联立解得??（1分）
AB过程：根据运动学公式?有
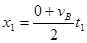?（1分）
时间?（1分）
（3）从圆环开始运动到最终静止在粗糙杆上通过的总路程为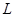
根据动能定理?有??（3分）
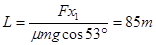总路程?（2分）
注：其他正确解法同样给分。

本题难度：一般