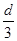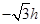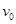1、计算题  如图所示，在直角坐标xoy内，在第1象限的区域I内存在垂直于纸面向外宽度为d的匀强磁场，区域Ⅱ内存在垂直于纸面向里宽度为的匀强磁场；在第三象限存在沿y轴正向的匀强电场，一质量为m带电量为+q的带电粒子从电场中的坐标为（-2h，）点以速度水平向右射出，经过原点O处射入区域I后垂直MN射入区域Ⅱ，（粒子的重力忽略不计）求：

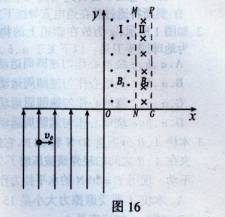
小题1:区域I内磁感应强度B1的大小；
小题2:若区域Ⅱ内磁感应强度B2的大小是B1的整数倍，当粒子再次回到y轴时坐标可能值为多少?

参考答案：
小题1: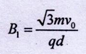
小题2: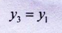

本题解析：

本题难度：一般

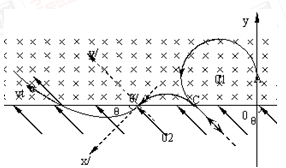
2、计算题  （18分）如图所示，x轴上方有一匀强磁场，磁感应强度为B，磁场方向垂直于纸面向里。X轴下方有一匀强电场，电场强度为E、方向与y轴的夹角θ=45°且斜向上方。现有一质量为m电量为q的正离子，以速度v0由y轴上的A点沿y轴正方向射入磁场，该离子在磁场中运动一段时间后从x轴上的C点（图中未画出）进入电场区域，离子经C点时的速度方向与电场方向相反。 不计离子的重力，设磁场区域和电场区域足够大， 求：

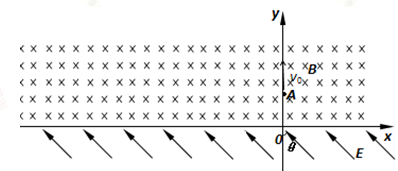
（1）C点的坐标；
（2）离子从A点出发到第三次穿越x轴时的运动时间；                       
（3）回答：离子从第三次过x轴到第四次过x轴的过程在做什么运动。并大致画出离子前四次穿越x轴在磁场和电场区域中的运动轨迹。

参考答案：（1）C点坐标为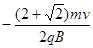（，0）。（2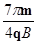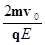）+；（3）类平抛运动，轨迹如下图：

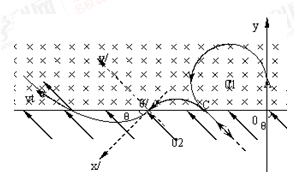
本题解析：（1）磁场中带电粒子在洛仑兹力作用下做圆周运动，故有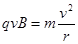                  ①
由几何知识知，xC＝ （r＋rcos450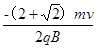）＝                     ③
故，C点坐标为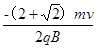（，0）               ③ 
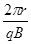（2）=          ④
设粒子从A到C的时间为t1，设粒子从A到C的时间为t1，由题意知
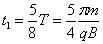                                    ⑤
设粒子从进入电场到返回C的时间为t2，其在电场中做匀变速运动，由牛顿第二定律和运动学知识，有   
                            ⑥

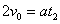及                ⑦
联立⑥⑦解得                  ⑧
设粒子再次进入磁场后在磁场中运动的时间为t3，由题意知
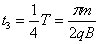                        ⑨
故而，设粒子从A点到第三次穿越x轴的时间为

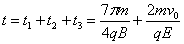
考点：带电粒子在电场中的运动（类平抛运动）、带电粒子在匀强磁场中的运动

本题难度：困难

3、选择题  地球大气层外有一层复杂的电离层，既分布有地磁场，也分布有电场.假设某时刻在该空间中有一小区域存在如图所示的电场和磁场；电场的方向在纸面内斜向左下方，磁场的方向垂直纸面向里.此时一带电宇宙粒子恰以速度v垂直于电场和磁场射入该区域，不计重力作用，则在该区域中，有关该带电粒子的运动情况可能的是(? )

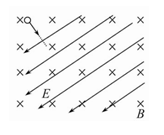
A．仍做直线运动
B．立即向左下方偏转
C．立即向右上方偏转
D．可能做匀速圆周运动

参考答案：选A、B、C.

本题解析：因Eq与Bqv二者开始时方向相反，当二者相等时，A正确；当Eq>Bqv时，向电场力方向偏，当Eq<Bqv时，向洛伦兹力方向偏，B、C正确；有电场力存在，粒子不可能做匀速圆周运动，D错.

本题难度：一般

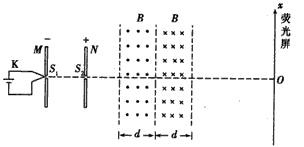
4、计算题  如图所示，M、N为两块带等量异种电荷的平行金属板，S1、S2为板上正对的小孔，N板右侧有两个宽度均为d的匀强磁场区域，磁感应强度大小均为B，方向分别垂直于纸面向外和向里，磁场区域右侧有一个荧光屏，取屏上与S1、S2共线的O点为原点，向上为正方向建立x轴。M板左侧电子枪发射出的热电子经小孔S1进入两板间，电子的质量为m，电荷量为e，初速度可以忽略。
(1)当两板间电势差为U0时，求从小孔S2射出的电子的速度v0；
(2)求两金属板间电势差U在什么范围内，电子不能穿过磁场区域打到荧光屏上：
(3)若电子能够穿过磁场区域而打到荧光屏上，试在图上定性地画出电子运动的轨迹；
(4)求电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系。

参考答案：解：(1)根据动能定理，得
解得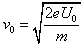
(2)欲使电子不能穿过磁场区域而打到荧光屏上，应有
而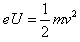，解得
(3)电子穿过磁场区域而打到荧光屏上时运动的轨迹如图所示

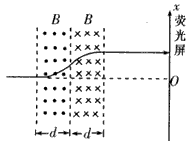
(4)若电子在磁场区域做圆周运动的轨道半径为r，穿过磁场区域打到荧光屏上的位置坐标为x，则由(3)巾的轨迹图可得
注意到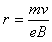和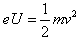
所以，电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系为

本题解析：

本题难度：困难

5、填空题  如图所示，质量为m，带电量为+q的粒子，从两平行电极板正中央垂直电场线和磁感线以速度v飞入。已知两板间距为d，磁感强度为B，这时粒子恰能直线穿过电场和磁场区域（重力不计）。今将磁感强度增大到某值，则粒子将落到极板上。当粒子落到极板上时的动能为______。

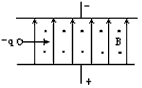
参考答案：(mv2-qdvB)/2

本题解析：

本题难度：一般