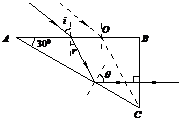
1、计算题  （9分） 如图所示，用折射率n=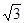的玻璃制成的三棱镜截面。平行光线由AB面入射，从BC面射出时光线与BC面垂直。则斜射到AB面上光线的入射角是多少？斜射到AB面上的光束，并能从BC面上射出的那部分光束宽度是AB边长的多少倍？

参考答案：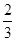

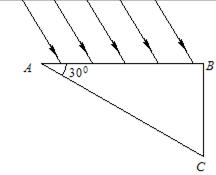
本题解析：要使光线从BC面射出时光线与BC面垂直，那么在三棱镜中的入射光线也必与BC面垂直，这样的入射光线只有经AC面全反射才能获得，如图所示。

此时：θ＝90°－30°＝60°　?（2分）
r ＝180°―90°― 30°―30°＝30°　（2分）
根据光的折射定律得：
sin i ＝n sin r ＝? i＝60°?（2分）
斜射到AB面上的光束，并能从BC面上射出的那部分光束的边界右图，其中射向AO段的能从BC面垂直射出，OB段则不能．
∵AB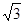＝BC，OB＝?
∴AB＝3 OB?（2分）
AO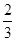＝?AB ?（1分）

本题难度：一般

2、选择题  甲、乙两种单色光分别垂直进入一块厚玻璃砖，已知它们通过玻璃中的时间t甲＞t乙，那么，甲乙两种单色光光子的能量关系是（　　）
A．E甲＞E乙
B．E甲＜E乙
C．E甲=E乙
D．不能确定

参考答案：光通过玻璃中的时间t=sv，而光在玻璃中传播速度为v=cn，则得t=nsc，c、s相同，则知折射率n∝t，可知玻璃对甲光的折射率较大，该光的频率较大，根据光子能量公式E=hγ得知，甲光子能量较大，故A正确．
故选A

本题解析：

本题难度：简单

3、计算题  如图所示，半圆玻璃砖的半径R=10cm，折射率为n=，直径AB与屏幕垂直并接触于A点。激光a以入射角i=30°射向半圆玻璃砖的圆心O，结果在水平屏幕MN上出现两个光斑。求：
（1）两个光斑之间的距离L；
（2）使透射光消失，入射角应的范围？（若sinθ=b，可表示为θ=arcsinb）

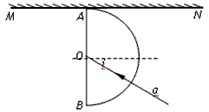
参考答案：解：（1）画出如图光路图，设折射角为r根据折射定律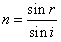
解得
由几何知识得，ΔOPQ为直角三角形，所以两个光斑PQ之间的距离：

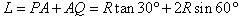
解得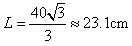
（2）i∈[arcsin，π/2]

本题解析：

本题难度：困难

4、计算题  如图所示，光线a从某种玻璃射向空气，在它们的界面MN上发生反射和折射，反射光线b和折射光线c刚好垂直，已知此时入射角为iB，求：

①玻璃的折射率n；
②若要光线c消失，入射角iC应为多大？

参考答案：①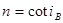②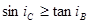

本题解析：①反射光线b和折射光线c刚好垂直，根据几何知识可得：折射角为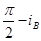，所以根据折射定律可得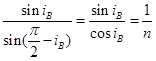：，故有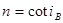，要光线c消失，即发生全反射，所以，解得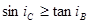

本题难度：一般

5、计算题  一列简谐横波沿x轴正向传播，波传到x=lm的P点时P点开始向y轴负方向振动，从此刻开始计时，已知在t=0.4s时PM间第一次形成图示波形，此时x=4m的M点正好在波谷。下列说法中正确的是（?）

A．这列波的传播速度是7.5m／s
B．t=0.5s时，x=5m处的质点Q（图中未画出），第一次到达波谷
C．当M点开始振动时，P点正好在波谷
D．P点的振动周期为0.4s
（2）（10分）如图所示，一束截面为圆形（半径R=lm）的平行紫光垂直射向一半径也为R的玻璃半球的平面，经折射后在屏幕S上形成一个圆形亮区，屏幕S至球心距离为D=m，不考虑光的干涉和衍射，试问：

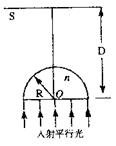
①若玻璃半球对紫色光的折射率为，请你求出圆形亮区的半径。
②若将题干中紫色改为白光，在屏幕S上形成的圆形亮区的边缘是什么颜色？

参考答案：34．（1）BD（5分）
（2）①如图，紫光刚要发生全反射时的临界光线射在屏幕S上的E点处，

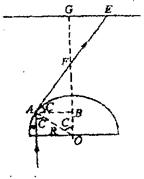
E点到亮区中心G的距离r就是所求最大半径。
设紫光临界角为C，则有?（1分）
由几何知识可知：AB=R·?（1分）
?（1分）
?（1分）
?（1分）
?（1分）
所以有：?（2分）
②紫色（2分）

本题解析：略

本题难度：一般