1、计算题  如图所示，倾角为θ的斜面上只有AB段粗糙，其余部分都光滑，AB段长为3L．有若干个相同的小方块沿斜面靠在一起，但不粘接，总长为L．将它们由静止释放，释放时下端距A为2L．当下端运动到A下面距A为L/2时物块运动的速度达到最大．（单独研究一个小方块时可将其视为质点）

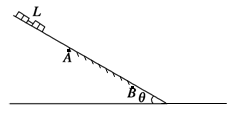
① 求物块与粗糙斜面的动摩擦因数；
② 求物块停止时的位置；
③ 要使所有物块都能通过B点，由静止释放时物块下端距A点至少要多远？　

参考答案：（1）μ＝2tanθ；（2）物块的下端停在B端；（3）s＝3L

本题解析：
试题分析: (1)当整体所受合外力为零时，整体速度最大，设整体质量为m，则
?
得μ＝2tanθ
(2)设物块停止时下端距A点的距离为x，根据动能定理
?
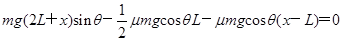解得x＝3L?
即物块的下端停在B端?
(3)设静止时物块的下端距A的距离为s，物块的上端运动到A点时速度为v，根据动能定理
?
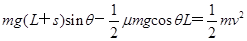物块全部滑上AB部分后，小方块间无弹力作用，取最上面一块为研究对象，设其质量为m0，运动到B点时速度正好减到0，根据动能定理
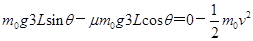?得s＝3L

本题难度：一般

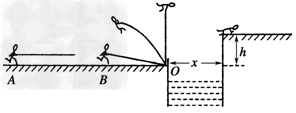
2、计算题  如图所示，一位质量m＝60?kg、参加“挑战极限运动”的业余选手，要越过一宽为x＝2.5?m的水沟后跃上高为h＝2.0?m的平台．他采用的方法是：手握一根长L＝3.25?m的轻质弹性杆一端，从A点由静止开始匀加速助跑，至B点时杆另一端抵在O点的阻挡物上，接着?杆发生形变，同时人蹬地后被弹起，到达最高点时杆处于竖直状态，人的重心在杆的顶端，此刻人放开杆水平飞出并趴落到平台上，运动过程中空气阻力可忽略不计． ? ?
(1)设人到达B点时速度vB＝8?m/s，人匀加速运动的加速度a＝2?m/s2，求助跑距离xAB；
(2)人要最终到达平台，在最高点飞出时刻的速度应至少多大？(g＝10?m/s2)
(3)设人跑动过程中重心离地高度H＝0.8?m，在(1)、(2)两问的条件下，在B点人蹬地弹起瞬间应至少再做多少功？

参考答案：解：(1)由运动学公式vB2＝2axAB，可得xAB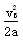＝＝16 m
(2)设人在最高点最小速度为v，人做平抛运动过程，有L－h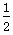＝gt2，x＝vt
解得v＝x·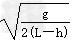＝5 m/s
(3)人从B点至最高点过程，由动能定理得W－mg(L－H)＝mv2－mvB2
解之W＝mg(L－H)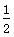＋mv2－mvB2＝300 J

本题解析：

本题难度：一般

3、计算题  如图所示，A、B两小球质量分别为mA=0.05kg、mB=0.lkg，用一根长为L=1.0rn的细绳连接，细绳是不能伸长的轻绳，A球套在一根斜放的粗糙杆上，杆与水平面夹角θ=300。起始，同时给A、B一个方向沿杆向下、大小相同的初速度，此后观察到A、B连线保持竖直。当A球运动到P点时，碰到钉子突然停下，B球继续运动，但沿绳方向的速度瞬间消失，只剩下垂直绳方向的速度，B球恰好能不与杆相碰，不计空气阻力，已知OP间的竖直高度为向h= l.0m，g取10m/s2，求：

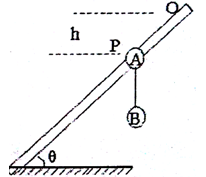
（1）A与杆接触面间的动摩擦因数μ。
（2）初速度v0的大小。
（3）整个过程中系统损失的机械能ΔE。

参考答案：（1）?（2）?（3）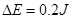

本题解析：（1）OP段，系统处于平衡状态，则


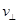
（2）A停止运动时，B以A为圆心沿切向一分速度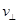摆起，法向分速度为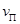即时突变为零，如图所示，
则
摆起过程，根据动能定理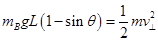
解得：
（3）根据能量守恒：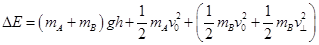
代入数据得：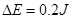

本题难度：一般

4、简答题  如图所示，在游乐节目中，要求选手从高为H的平台上A点由静止出发，沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出，最后刚好落到水池中的浮台上．设滑道可以伸缩，其水平距离为L，B点的高度h可由选手自由调节（取g=10m/s2）．要求：

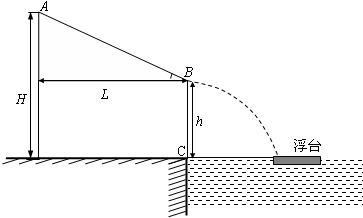
（1）选手到达B点的速度表达式；
（2）试证明选手落到浮台上的速度大小与B点的高度h无关；
（3）同学甲认为B点的高度h越大，选手在空中飞越的时间越长，在浮台上的落点距岸边C越远；同学乙认为B点的高度h越小，选手到达B点的水平速度越大，在浮台上的落点距岸边C越远，请通过推算说明你的观点．

参考答案：（1）由A运动到B过程，设滑道倾角为θ，
则由牛顿第二定律得：mgsinθ-μmgcosθ=ma
又：vB2-0=2aLcosθ
且：tanθ=H-hL
解得：vB=

本题解析：

本题难度：一般

5、计算题  如图所示，摩托车运动员从高度h=5m的高台上水平飞出，跨越L=10m的壕沟。摩托车以初速度v0从坡底冲上高台的过程历时t=5s，发动机的功率恒为P=1.8kW。已知人和车的总质量为m=180kg（可视为质点），忽略一切阻力。取g=10m/s2。
（1）要使摩托车运动员从高台水平飞出刚好越过壕沟，求他离开高台时的速度大小。
（2）欲使摩托车运动员能够飞越壕沟，其初速度v0至少应为多大？
（3）为了保证摩托车运动员的安全，规定飞越壕沟后摩托车着地时的速度不得超过26m/s，那么，摩托车飞离高台时的最大速度vm应为多少？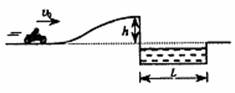

参考答案：（1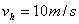）（2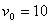）（3）24m/s

本题解析：（1）摩托车运动员由高台水平飞出后由平抛运动规律：
水平方向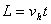?①
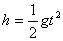竖直方向?②
联立①②得?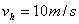
（2） 摩托车运动员由坡底冲上高台，根据动能定理
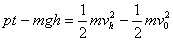?③
将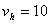m/s代入到③得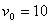m/s?
（3）从高台水平飞出到地面，由机械能守恒定律
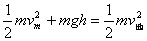?④
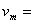解得24m/s
点评：要求我们能根据不同的过程选用不同的物理规律；对于平抛等只受重力的运动过程，优先采用机械能守恒定理．

本题难度：一般