1、选择题  质量为m的小球A在光滑的水平面上以速度v0与质量为2m的静止小球B发生正碰，碰后A球的动能恰好变为原来的1/9，则B球速度大小可能是（　　）
A．

参考答案：根据碰后A球的动能恰好变为原来的19得：
12mv2=19?12mv02
v=±v03
碰撞过程中AB动量守恒，则
mv0=mv+2mvB
解得：vB=v03或vB=2v03
故选AD．

本题解析：

本题难度：简单

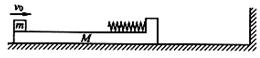
2、计算题  质量M=3kg的长木板静止在光滑水平面上，木板左侧放置一质量m=1kg的木块，右侧固定一轻弹簧，处于原长状态，弹簧正下方部分的木板上表面光滑，其他部分的木板上表面粗糙，如图所示现给木块v0=4m/s的初速度，使之向右运动，在木板与木块向右运动过程中，当木板和木块达到共速时，木板恰与墙壁相碰，碰撞过程时间极短，木板速度的方向改变，大小不变，最后木块恰好在木板的左端与木板相对静止。求：
①木板与墙壁相碰时的速度v1；
②整个过程中弹簧所具有的弹性势能的最大值Epm；

参考答案：①1m/s.?②3.75J

本题解析：①以木块与木板组成组成的系统为研究对象，从木块开始运动到两者速度相同的过程中，系统动量守恒，由动量守恒定律可得：mv0=（M+m）v1,解得：v1=1m/s.
②木板与墙壁碰后返回，木块压缩弹簧，当弹簧压缩到最短时，木块与木板速度相等，在此过程中两者组成的系统动量守恒，由动量守恒定律可得：Mv1-mv1=（M+m）v2,解得：v2=0.5m/s;
当弹簧压缩到最短时，弹性势能最大，由动能定理可得：

当木块到达木板最左端时两者速度相等，在此过程中，系统动量守恒，由动量守恒定律可得：，解得v3=0.5m/s;
从木块开始运动到木块回到木板最左端的整个过程中，由能量守恒定律可知: ，解得：Q=3.75J，EPm=3.75J.

本题难度：一般

3、简答题  [物理选修3-5模块]
（1）激光制冷原理可以根据如图所示的能级图简单说明，激光射入介质中，引起介质中的离子从基态跃迁到激发态n=11，一些处于激发态n=11的离子很快吸收热量转移到激发态n=12，离子从激发态n=11和n=12向基态跃迁辐射两种荧光，部分辐射荧光的能量大于入射激光的能量，上述过程重复下去实现对介质的冷却，下列说法正确的是______
A．两种辐射荧光波长都大于射入介质的激光波长
B．激光制冷过程中，介质内能减少量等于辐射荧光与吸收激光的能量差
C．两种辐射荧光在同一装置下分别做双缝干涉实验，相邻两条亮条纹间的距离不相等
D．若两种辐射荧光分别照射同一金属板都能产生光电效应，则光电子的最大初动能相等
（2）在光滑的水平地面上静止着一质量为M=0.4kg的薄木板，一个质量为m=0.2kg的木块（可视为质点）以υ0=4m/s的速度从木板左端滑上，一段时间后，又从木板上滑下（不计木块滑下时机械能损失），两物体仍沿直线继续向前运动，从木块与木板刚刚分离开始计时，经时间t=3.0s，两物体之间的距离增加了x=3m，已知木块与木板的动摩擦因数μ=0.4，求薄木板的长度．

参考答案：（1）A、根据玻尔理论和光子的能量公式E=hcλ分析可知，从n=12向基态跃迁辐射的荧光波长小于射入介质的激光波长．故A错误．
B、激光制冷过程中，由玻尔理论得知，介质内能减少量等于辐射荧光与吸收激光的能量差．故B正确．
C、干涉条纹的间距与波长成正比．则两种辐射荧光在同一装置下分别做双缝干涉实验，相邻两条亮条纹间的距离不相等．故C正确．
D、产生光电效应时，光电子的最大初动能随着入射光的频率的增大而增大，由于两种荧光频率不等，则光电子的最大初动能不相等．故D错误．
故选BC．
（2）设木块与木板分离后速度分别为为：v1、v2，由动量守恒定律得：
mv0=mv1+Mv2
根据题意，有：
v1-v2=St
解得：v1=2m/s，v2=1m/s
根据动能定理得：μmgd=12mv20-12mv21-12Mv22
代入数据解得：
d=1.25m
即薄木板的长度为1.25m．
故答案为：
（1）BC；（2）薄木板的长度是1.25m．

本题解析：

本题难度：一般

4、简答题  如图所示，长为L的木板A右边固定着一个挡板，包括挡板在内的总质量为1.5M，静止在光滑的水平地面上。有一质量为M的小木块B，从木板A的左端开始以初速度v0在
木板A上滑动。小木块B与木板A间摩擦因数为μ，小木块B滑到木板A的右端与挡板发生碰撞。已知碰撞过程时间极短，且碰后木块B恰好滑到木板A的左端就停止滑动。
（1）若μL=3v02/160g，在小木块B与挡板碰撞后的运动过程中，摩擦力对木板A做正功还是负功？做了多少？
（2）讨论木板A和小木块B在整个过程中，是否有可能在某一段时间内相对地面运动方向是向左的。如果不可能，说明理由；如果可能，求出至少可能向左滑动、又能保证木板A和小木块B刚好不脱离的条件。

参考答案：
（1）摩擦力对木板做负功，大小为（27/400）M v02
（2）B向左滑又不脱离A的条件是2v02/15g＜μL≤3v02/20g

本题解析：（1）设B与A碰撞后A、B的速度分别为vA、vB，最终A、B的共同速度为v，则由动量守恒、能量守恒有mBv0=mAvA+mBvB，mBv0=（mA+mB）v
μmBgL=（1/2）mAvA2+（1/2）mBvB2-（1/2）（mA+mB）v2
又μL=3v02/160g
以上各式联列解得v=（2/5）v0，vA=（1/2）v0，vB=（1/4）v0
或v=（2/5）v0，vA=（3/10）v0，vB=（11/20）v0
分析上述两组结果，由于两物碰撞后均与v0同向，而其中第二组结果vA=（3/10）v0＜vB=（11/20）v0，该速度关系与实际不符，舍去
因此，由动能定理可得摩擦力做功
Wf =（1/2）（1.5M）v2-（1/2）（1.5M）vA2=-（27/400）M v02
即摩擦力对木板做负功，大小为（27/400）M v02
（2）整个过程动量守恒，A不可能向左运动，碰后B可能。
要使B向左运动，由动量守恒、能量守恒有
mBv0=mAvA+mBvB，mBv0=（mA+mB）v
μmBgL=（1/2）mAvA2+（1/2）mBvB2-（1/2）（mA+mB）v2? vB＜0
以上各式联列解得μL＞2v02/15g
要保证A和B不脱离，由动量守恒和能量守恒有
mBv0=（mA+mB）v
2μmBgL≥（1/2）mBv02-（1/2）（mA+mB）v2
解得μL≤3v02/20g
故B向左滑又不脱离A的条件是2v02/15g＜μL≤3v02/20g

本题难度：一般

5、选择题  冰壶运动深受观众喜爱，图1为2014年2月第22届索契冬奥会上中国队员投掷冰壶的镜头。在某次投掷中，冰壶甲运动一段时间后与对方静止的冰壶乙发生正碰，如图2。若两冰壶质量相等，则碰后两冰壶最终停止的位置，可能是图3中的哪幅图?

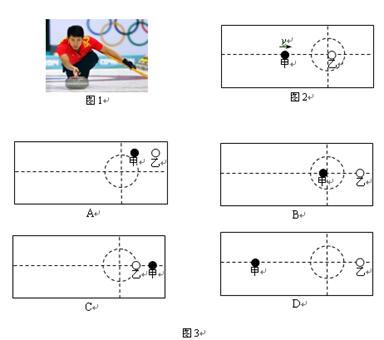
参考答案：B

本题解析：冰壶甲乙碰撞过程动量守恒，碰撞前系统动量水平向右，碰撞后合动量也必然水平向右，碰撞后冰壶在摩擦力作用下做匀减速直线运动，所以碰撞点即圆心到最后停靠点的连线代表碰撞后的速度方向，连线的长短代表碰撞后的速度大小。A图中，甲乙碰后的动量都斜向右上方，所以合动量不可能水平向右，不满足动量守恒定律选项A错。乙图中，碰撞后甲静止，乙水平向右运动，符合质量相等小球发生完全弹性碰撞的过程，选项B是可能的。选项C中，虽然甲乙动量都是水平向右，合动量也满足水平向右，但甲在后，乙在前，碰后甲不可能速度大于乙，即甲不可能在乙前面，选项C错。D选项，碰后甲的速度大于乙的速度，合动量水平向左，不符合动量守恒定律选项D错。

本题难度：一般