1、简答题  探究某种笔的弹跳问题时，把笔分为轻质弹簧、内芯和外壳三部分，其中内芯和外壳质量分别为m和4m．笔的弹跳过程分为三个阶段：

①把笔竖直倒立于水平硬桌面，下压外壳使其下端接触桌面（图a）；
②由静止释放，外壳竖直上升至下端距桌面高度为h1时，与静止的内芯碰撞（图b）；
③碰后，内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度为h2处（图c）．
设内芯与外壳的撞击力远大于笔所受重力、不计摩擦与空气阻力，重力加速度为g．求：
（1）外壳与内芯碰撞后瞬间的共同速度大小；
（2）从外壳离开桌面到碰撞前瞬间，弹簧做的功；
（3）从外壳下端离开桌面到上升至h2处，笔损失的机械能．

参考答案：设外壳上升高度h1时速度为V1，外壳与内芯碰撞后瞬间的共同速度大小为V2，
（1）对外壳和内芯，从撞后达到共同速度到上升至h2处，应用动能定理有：
（4m+m）g（?h2-h1）=12（4m+m）V22，
解得V2=

本题解析：

本题难度：一般

2、简答题  如图所示，某人通过一根跨过定滑轮的轻绳提升一个质量为m的重物，开始时人在滑轮的正下方，绳下端A点离滑轮的距离为H．人由静止拉着绳向右移动，当绳下端到B点位置时，人的速度为v，绳与水平面夹角为θ．问在这个过程中，人对重物做了多少功？

参考答案：人移动时对绳的拉力不是恒力，重物不是做匀速运动也不是做匀变速运动，故无法用W=Fscosθ求对重物做的功，需从动能定理的角度来分析求解．
当绳下端由A点移到B点时，重物上升的高度为：h=Hsinθ-H=H(1-sinθ)sinθ
重力做功的数值为：WG=mgH(1-sinθ)sinθ
当绳在B点实际水平速度为v时，v可以分解为沿绳斜向下的分速度v1和绕定滑轮逆时针转动的分速度v2，其中沿绳斜向下的分速度v1和重物上升速度的大小是一致的，




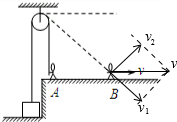
从图中可看出：v1=vcosθ
以重物为研究对象，根据动能定理得：W人-WG=12mv21-0
解得：W人=mgH(1-sinθ)sinθ+mv2cos2θ2
答：在这个过程中，人对重物做的功为mgH(1-sinθ)sinθ+mv2cos2θ2．

本题解析：

本题难度：一般

3、选择题  如图所示，两个质量不同的滑块，先后从同一光滑斜面的同一位置A处由静止滑下，则

A．两滑块在A处的重力势能相等
B．两滑块滑到斜面底端时的动能相等
C．两滑块滑到斜面底端时的速度相等
D．滑动过程中两滑块的加速度相等。

参考答案：CD

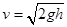本题解析：重力势能与物体的质量，高度有关还和零势能点的选取有关，所以A错。两物块从A处滑落到斜面底端这个过程中只有重力作功即得，滑到底端的速度和质量无关，两速度相等，故C对，而到底端时的动能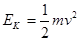，速度相等，但质量不等，所以动能不等，故B错，设斜面的倾斜角为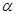，则物体重力沿斜面向下的分力，则下滑的加速度为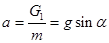?和质量无关，所以滑动过程中两滑块的加速度相等，D对。

本题难度：一般

4、选择题  如图所示，圆弧虚线表示正点电荷电场的等势面，相邻两等势面间的电势差相等。光滑绝缘直杆沿电场方向水平放置并固定不动，杆上套有一带正电的小滑块（可视为质点），滑块通过绝缘轻弹簧与固定点O相连，并以某一初速度从M点运动到N点，OM＜ON。若滑块在M、N时弹簧的弹力大小相等，弹簧始终在弹性限度内，则

[? ]
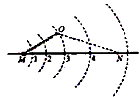
A．滑块从M到N的过程中，速度可能一直增大
B．滑块从位置1到2的过程中，电场力做的功比从位置3到4的小
C．在M、N之间的范围内，可能存在滑块速度相同的两个位置
D．在M、N之间可能存在只由电场力确定滑块加速度大小的三个位置

参考答案：AC

本题解析：

本题难度：一般

5、选择题  质量为m的物体，在距地面h高处以g/3的加速度由静止竖直下落到地面，下列说法中正确的是（　　）
A．重力做功mgh/3
B．物体的重力势能减少mgh/3
C．物体的动能增加2mgh/3
D．物体的机械能减少2mgh/3

参考答案：A、在下落的过程中，重力做功W=mgh，重力势能减小mgh．故A、B错误．
C、物体所受的合力为13mg，则合力做功为13mgh，根据动能定理知，动能的增加量为13mgh．故C错误．
D、重力势能减小mgh，动能的增加量为13mgh，则机械能减小23mgh．故D正确．
故选D．

本题解析：

本题难度：一般