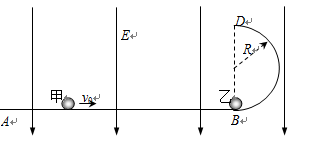
1、计算题 如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103V/m。一不带电的绝缘小球甲,以速度υ0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞。已知乙球的质量为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,甲球质量为乙球质量的k倍,g取10m/s2。(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)
【小题1】若k=1,且甲乙两球碰撞后,乙恰能通过轨道的最高点D,求甲的速度υ0;
【小题2】若k>1,且甲仍以(1)中的速度υ0向右运动,求乙在轨道上的首次落点到B点的距离范围。
参考答案:
【小题1】
【小题2】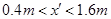
本题解析:(1)在乙恰能通过轨道的最高点的情况下,设乙到达最高点的速度为vD,乙离开D点到达水平轨道的时间为t,乙的落点到B点的距离为x,则ks5u
 ① (1分)
① (1分)
设碰撞后甲、乙的速度分别为v甲、v乙,根据动量守恒和机械能守恒定律有:
 ② (1分)
② (1分)
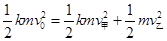 ③ (1分)
③ (1分)
联立②③得: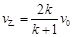 ④ (1分)
④ (1分)
由k=1,则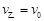
由动能定理得: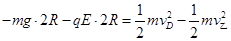 ⑤ (1分)
⑤ (1分)
联立①④⑤得:  ⑥ (1分)
⑥ (1分)
(2)甲、乙完全弹性碰撞,碰撞后甲、乙的速度分别为v甲、v乙,由②③得
解得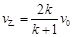 ⑦ (1分)
⑦ (1分)
又k>1,则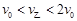 ⑧ (1分)
⑧ (1分)
设乙球过D点的速度为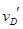 ,由动能定理得
,由动能定理得
 ⑨ (1分)
⑨ (1分)
解得: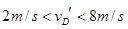 ⑩ (1分)
⑩ (1分)
设乙在水平轨道上的落点到B点的距离为 ,则有:
,则有:
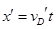 11
11
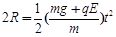 12 (1分)
12 (1分)
联立121314得: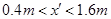 (1分)
(1分)
本题难度:困难
2、填空题 一人从高处坠下,当人下落H高度时安全带刚好绷紧,人又下落h后人的速度减为零,设人的质量为M,则绷紧过程中安全带对人的平均作用力为 。
参考答案:mg(H+h)/h
本题解析:略
本题难度:一般
3、填空题 物体A、B的质量之比为mA:mB=4:1,使它们以相同的初速度沿水平地面滑行,若它们受到的阻力相等,那么它们停下来所用的时间之比为tA:tB=______,若两物体与地面的动摩擦因数相同,那么它们停下来所用的时间之比为tA:tB=______
参考答案:4:1;1:1
本题解析:(1)假设阻力大小为f,则

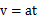
可得: 因为具有相同的初速度和阻力,所以
因为具有相同的初速度和阻力,所以
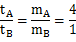
(2)假设动摩擦因数大小为 ,则
,则
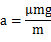
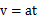
可得: 因为具有相同的初速度和动摩擦因数,所以
因为具有相同的初速度和动摩擦因数,所以
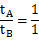
本题难度:一般
4、填空题 如图1—6所示,质量为m的物体沿1/4圆弧无初速度滑下,圆弧的半径为R,A点与圆心O等高,滑至最低点B时的速度为V,则下滑过程中,重力做的功为 ,物体克服阻力做的功为 。
参考答案:mgR,mgR-mV2/2
本题解析:由WG=mgh可得WG=mgR,由动能定理WG-WF= mV2/2求得WF= mgR-mV2/2
本题难度:一般
5、选择题 一人用力把质量为1 kg的物体由静止向上提高1 m,使物体获得4 m/s的速度,则下列说法中正确的是( )(g="10" m/s2)
A.人对物体做功为18 J
B.物体重力做功为10 J
C.合外力对物体做的功为10 J
D.物体动能改变为8 J