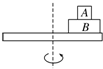
1、简答题  如图，板长为l、间距为d的平行金属板水平放置，两板间所加电压大小为U，在极板的右侧相距为a处有与板垂直的足够大光屏PQ，一带正电的粒子以初速度v0从两板正中间平行两板射入，从两板间射出时速度的偏转角为37°，不计粒子受到的重力．（cos37°=0.8，sin37°=0.6）

（1）求粒子的比荷q/m；
（2）若在两板右侧MN和光屏PQ间加如图所示的磁场，要使粒子不打在光屏上，求磁感应强度B大小的取值范围；
（3）若在两板右侧MN和光屏PQ间加垂直纸面向外、大小为E0的匀强电场，设初速度方向所在直线与光屏交点为O点，取O点为坐标原点，水平向右为x正方向，垂直纸面向外为z轴的正方向，建立如图所示的坐标系，求粒子打在光屏上的坐标（x，y，z）．

参考答案：（1）由题意知，粒子在电场中偏转时做类平抛运动，设粒子从两版间射出时，速度的水平分量为vx，竖直分量为vy则由题意有：
vx=v0
vy=at=qUmd×lv0=qUlmdv0
又因为粒子从电场射出时速度的偏转角为37°?则有：tan370=vyv0=qUlmdv20
解之得：qm=3dv204Ul
（2）由题意得，粒子进入磁场的速度vcos37°=v0得v=54v0
设粒子刚好打在光屏时，磁感应强度为B，



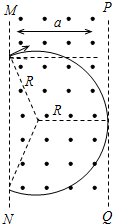
如图，由几何知识有：Rsin37°+R=a 得：R=a1+sin37°
粒子在磁场中做圆周运动，洛伦兹力提供向心力有：Bqv=mv2R
?得：B=mvqR=1qm×54v0a1+sin37°=8Ul3dv0a
所以，要使粒子不大在光屏上，应有磁感应强度小于8Ul3dv0a
（3）由题知：
微粒只要打在屏上，x坐标就为0?
微粒在y轴方向先做匀加速直线运动，后做匀速直线运动，根据几何关系可得：
y=(l2+a)tan37°=3l+6a8
微粒在z轴方向在电场力作用下做初速度为0的匀加速直线运动，根据位移时间关系有：
z=12×qE0m×t2?
根据运动的等时性有在z轴方向运动时间t=av0
代入得：z=3E0da28Ul（1分）
则坐标为：（0，3l+6a8，3E0da28Ul）
答：（1）粒子的比荷qm=3dv204Ul；
（2）若在两板右侧MN和光屏PQ间加如图所示的磁场，要使粒子不打在光屏上，磁感应强度小于8Ul3dv0a；
（3）若在两板右侧MN和光屏PQ间加垂直纸面向外、大小为E0的匀强电场，设初速度方向所在直线与光屏交点为O点，取O点为坐标原点，水平向右为x正方向，垂直纸面向外为z轴的正方向，建立如图所示的坐标系，粒子打在光屏上的坐标：（0，3l+6a8，3E0da28Ul）．

本题解析：

本题难度：一般

2、简答题  一个3Kg的物体在半径为2m的圆周上以4m/s的线速度运动，所需向心力是______N．

参考答案：根据F=mv2r得：所需向心力F=3×162=24N
故答案为24

本题解析：

本题难度：一般

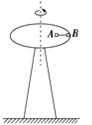
3、计算题  如图所示，水平转台高1.25 m，半径为0.2 m，可绕通过圆心处的竖直转轴转动．转台的同一半径上放有质量均为0.4 kg的小物块A、B(可看成质点)，A与转轴间距离为0.1 m，B位于转台边缘处，A、B间用长0.1 m的细线相连，A、B与水平转台间最大静摩擦力均为0.54 N，g取10 m/s2。
(1)当转台的角速度达到多大时细线上出现张力？
(2)当转台的角速度达到多大时A物块开始滑动？
(3)若A物块恰好将要滑动时细线断开，此后转台保持匀速转动，求B物块落地瞬间A、B两物块间的水平距离．(不计空气阻力，计算时取π＝3)

参考答案：解：(1)由Ff＝mω2r可知，B先达到临界状态，故当满足Ffm<mω12r时线上出现张力
解得ω1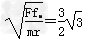＝rad/s
(2)当ω继续增大，A受力也达到最大静摩擦力时，A开始滑动
Ffm－FT＝mω′2r/2
Ffm＋FT＝mω′2r
得ω′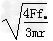＝=3?rad/s
(3)细线断开后，B沿水平切线方向飞出做平抛运动
由h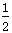＝gt2得t＝0.5?s
vB＝ωr＝0.6?m/s
可得B的水平射程xB＝vBt＝0.3?m
细线断开后，A相对静止于转台上，t时间转过角度θ＝ωt＝1.5?rad即90°
故AB间水平距离lx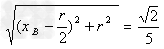＝=0.28?m（0.3均可）

本题解析：

本题难度：一般

4、选择题  如图所示，物体A、B随水平圆盘绕轴匀速转动，物体B在水平方向所受的作用力有（　　）
A．圆盘对B及A对B的摩擦力，两力都指向圆心
B．圆盘对B的摩擦力指向圆心，A对B的摩擦力背离圆心
C．圆盘对B及A对B的摩擦力和向心力
D．圆盘对B的摩擦力和向心力