1、计算题 (18分)如图,圆形玻璃平板半径为R,离水平地面的高度为h,可绕圆心O在水平面内自由转动,一质量为m的小木块放置在玻璃板的边缘.玻璃板匀速转动使木块随之做匀速圆周运动.
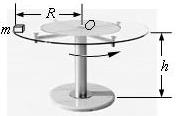
(1)若已知玻璃板匀速转动的周期为T,求木块所受摩擦力的大小.
(2)缓慢增大转速,木块随玻璃板缓慢加速,直到从玻璃板滑出.已知木块脱离时沿玻璃板边缘的切线方向水平飞出,落地点与通过圆心O的竖直线间的距离为s.木块抛出的初速度可认为等于木块做匀速圆周运动即将滑离玻璃板时的线速度,滑动摩擦力可认为等于最大静摩擦力,试求木块与玻璃板间的动摩擦因数μ.
参考答案:(1) ?(2)
?(2)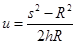
本题解析:(1)木块所受摩擦力等于木块做匀速圆周运动的向心力
 ?①(3分)
?①(3分)
(2)木块做匀速圆周运动即将滑离玻璃板时,静摩擦力达到最大,有
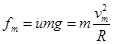 ?②(3分)
?②(3分)
木块脱离玻璃板后在竖直方向上做自由落体运动,有
 ?③(3分)
?③(3分)
在水平方向上做匀速运动,水平位移
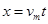 ?④(3分)
?④(3分)
x与距离s、半径R的关系如图所示,

由图可得(图1分)
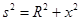 ?⑤(2分)
?⑤(2分)
由以上各式解得木块与玻璃板间的动摩擦因数?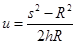 ?⑥(3分)
?⑥(3分)
本题难度:一般
2、选择题 在验证牛顿第二定律关于作用力一定时,加速度与质量成反比的实验中,以下做法错误的是(?)
A.平衡摩擦力时,应将装砂的小桶用细绳通过定滑轮系在小车上
B.每次改变小车的质量时,不需要重新平衡摩擦力
C.实验时,先放开小车,再接通打点计时器电源
D.小车运动的加速度可从天平测出装砂小桶和砂的质量(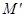 和
和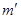 )以及小车质量M [(
)以及小车质量M [(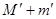 )<<M],直接用公式a=
)<<M],直接用公式a=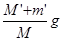 求出
求出
参考答案:ACD
本题解析:分析:在该实验中绳子的拉力就等于小车所受的合外力,故要平衡摩擦力,且不能悬挂装砂的小桶,但应该连接纸带且让纸带穿过打点计时器.平衡摩擦力就是让小车所受的滑动摩擦力等于小车的重力沿斜面的分力.为节约纸带应先接通电源待打点稳定后再放开小车.只能用纸带上的点求小车运动的加速度.
解答:解:A、在该实验中,我们认为绳子的拉力就等于小车所受的合外力,故在平衡摩擦力时,细绳的另一端不能悬挂装砂的小桶,故A错误.
B、由于平衡摩擦力之后有Mgsinθ=μMgcosθ,故tanθ=μ.所以无论是否改变小车的质量,小车所受的滑动摩擦力都等于小车的重力沿斜面的分力.故B正确.
C、由于在刚刚接通电源的瞬间打点计时器打点并不稳定,故应该先接通打点计时器电源待打点稳定后再放开小车,以节约纸带,故C错误.
D、D选项的方法成立的前提是牛顿第二定律即加速度与质量成反比,而本实验中我们是验证牛顿第二定律,故发生了循环论证,所以D是错误的.
本题是选错误的做法,故选ACD.
点评:在学习中D选项最容易出错,因为该选项中的方法是用牛顿第二定律验证牛顿第二定律,故不允许.
本题难度:简单
3、选择题 质量为m的木块位于粗糙水平桌面上,若用大小为F的水平恒力拉木块,其加速度大小为a。当拉力方向不变,大小变为2F时,木块的加速度大小为a′,则
[? ]
A.a′=a
B.a′<2a
C.a′>2a
D.a′=2a
参考答案:C
本题解析:
本题难度:一般
4、简答题 如图所示,是双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面.若女运动员做圆锥摆运动时和竖直方向的夹角为θ,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求这时男运动员对女运动员的拉力大小及两人转动的角速度.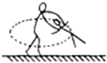
参考答案:以女运动员为研究对象,分析受力情况,作出力图,如图.

则女运动员受到的拉力F=mgcosθ
根据向心力公式有:
Fn=mω2r
解得:ω=
本题解析:
本题难度:一般
5、选择题 如图所示,质量为m的物体置于水平地面上,所受水平拉力F在2s时间内的变化图象如图甲所示,其运动的速度图象如图乙所示,g=10 m/s2。下列说法正确的是
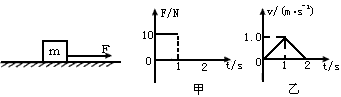
[? ]
A.物体和地面之间的动摩擦因数为0.1
B.水平拉力F的最大功率为5W
C.2s末物体回到出发点
D.2s内物体的加速度不变
参考答案:A
本题解析:
本题难度:一般