1、选择题  作用于同一物体上的两个力，F1＝5 N，F2＝4 N，它们的合力不可能是
A.9 N
B.5 N
C.2 N
D.10 N

参考答案：D

本题解析：

本题难度：困难

2、选择题 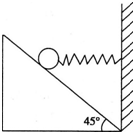 如图所示，为一位于墙角的光滑斜面，其倾角为45°，劲度系数为k的轻弹簧一端系在质量为m的小球上，另一端固定在墙上，弹簧水平放置．小球在斜面上静止时，弹簧的形变量大小为
A.
B.
C.
D.

参考答案：A

本题解析：分析：小球静止在斜面上，合力为零，分析小球的受力情况，根据平衡条件求解弹簧的弹力，即可由胡克定律求出弹簧的形变量．
解答：对小球受力如图所示，受到重力mg、斜面的支持力FN和弹簧的弹力F作用下处于平衡状态，故斜面的支持力FN和弹簧的弹力F的合力与mg等大、反向，则得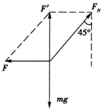
? F=mgtan45°=mg
又由胡克定律得
? kx=F
解得，弹簧的形变量大小x=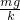
故选A
点评：本题是共点力平衡问题，正确分析受力是解题的关键，要规范地作出受力示意图，结合平衡条件的推论求解．

本题难度：困难

3、选择题  一根轻绳能承受的最大拉力为G，现将一重为G的物体系在绳的中点，两手先并拢分别握住绳的两端，然后缓慢对称左右分开．若想绳子不断，两绳之间的夹角不能超过
A.45°
B.60°
C.120°
D.135°

参考答案：C

本题解析：随着两绳之间夹角的增大，绳的拉力逐渐增大，当夹角为120°时，绳的拉力等于重物的重力G，随后绳的拉力继续增大直到断裂，故选项C正确．

本题难度：困难

4、选择题  如图所示，有一轻杆AO，O恰为圆弧的圆心，长为尺，可绕A自由转动．绳的一端悬挂一个重为6的物体，另一端通过杆的O端系在圆弧形墙壁上的C点．当系住点C由图示位置沿圆弧缓慢向上移动到B的过程中，OC绳所受拉力的大小变化情况是
A.逐渐减小
B.逐渐增大
C.先减小后增大
D.先增大后减小

参考答案：C

本题解析：分析：先对G受力分析可知竖直绳上的拉力不变，再对结点O分析可得出受力的平行四边形；根据C点的移动利用图示法可得出OC拉力的变化．
解答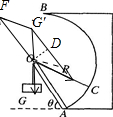：解：对G分析，G受力平衡，则拉力等于重力；故竖直绳的拉力不变；
再对O点分析，O受绳子的拉力OA的支持力及OC的拉力而处于平衡；受力分析如图所示；
将F和OC绳上的拉力合力，其合力与G大小相等，方向相反，则在OC上移的过程中，平行四边形的对角线保持不变，平行四边形发生图中所示变化，则由图可知OC的拉力先减小后增大，图中D点时力最小；
故选C．
点评：本题利用了图示法解题，解题时要注意找出不变的量作为对角线，从而由平行四边形可得出拉力的变化．

本题难度：简单

5、选择题  下列各组共点的三个力，可能平衡的有
A.3?N、4?N、8?N
B.3?N、5?N、1?N
C.4?N、7?N、8?N
D.7?N、9?N、16?N

参考答案：CD

本题解析：分析：三力平衡时，三力可以组成首位相连的三角形，故要使三力的合力为零，应保证任意两力之和可以大于等于第三力，任意两力之差小于等于第三力．
解答：A、3N与4N的合力最大值为7N，最小值为1N，不可以与8N的力平衡，故A错误；
B、3N和5N合成时，最大8N，最小2N，不可能与1N合成，故B错误；
C、4N和7N合成时，最大11N，最小3N，可能与8N合成，达到平衡；故C正确；
D、7N和9N的合力最小为2N，最大是16N，故可以与16N的力平衡，故D正确；
故选CD．
点评：判断三力能否平衡可以利用数学中三边组成平行三角形的方法，只要三边能组成三角形，则合力一定能为零．

本题难度：一般