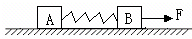
1、简答题  有一匀强电场，其场强为E，方向竖直向下．把一个半径为r的光滑绝缘环，竖直置于电场中，环面平行于电场线，环的顶点A穿有一个质量为m、电量为q（q＞0）的空心小球，如图所示．当小球由静止开始从A点下滑到最低点B时，小球受到环的压力多大？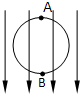

参考答案：设小球到达B点时的速度为V，由动能定理得(mg+qE)?2r=12mv2…①
在B点处由牛顿第二定律得N-mg-qE=mv2r…②
联立①和②式，解得小球在B点受到环的压力为：N=5（mg+qE）
答：小球受到环的压力5（mg+qE）．

本题解析：

本题难度：一般

2、计算题  （14分）如图，倾角为θ的斜面固定在水平地面上（斜面底端与水平地面平滑连接），A点位于斜面底端，AB段斜面光滑，长度为s，BC段足够长，物体与BC段斜面、地面间的动摩擦因数均为μ。质量为m的物体在水平外力F的作用下，从A点由静止开始沿斜面向上运动，当运动到B点时撤去力F。求：

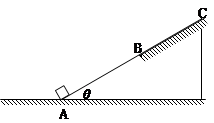
（1）物体上滑到B点时的速度vB；
（2）物体最后停止时距离A点的距离。

参考答案：（1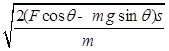）（2）若mgsinθ≤μmgcosθ时，物体最后停止时距离A点的距离?．若mgsinθ＞μmgcosθ时，最后在水平面上滑行的距离为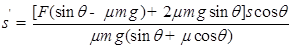

本题解析：（1）对于物体从A到B的过程，由动能定理得：

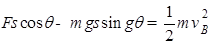
则得：
（2）设物体运动到最高点时距离A点的距离为x．对整个过程，由动能定理得：
Fscosθ-mgxsinθ-μmg（x-s）cosθ=0
解得：?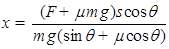
若mgsinθ≤μmgcosθ时，物体最后停止时距离A点的距离?．
若mgsinθ＞μmgcosθ时，物体下滑，设最后在水平面上滑行的距离为S′．对全过程，由动能定理得：
Fs-2μmg（x-s）cosθ-μmgS′=0
则得：

本题难度：一般

3、选择题  如图所示，一轻弹簧左端与物体A相连，右端与物体B相连，开始时，A、B均在粗糙水平面上不动，弹簧处于原长状态．在物体B上作用一水平向右的恒力F，使物体A、B向右运动．在此过程中，下列说法中正确的为（　　）
A．合外力对物体A所做的功等于物体A的动能增量
B．外力F做的功与摩擦力对物体B做的功之和等于物体B的动能增量
C．外力F做的功及摩擦力对物体A和B做功的代数和等于物体A和B的动能增量及弹簧弹性势能增量之和
D．外力F做的功加上摩擦力对物体B做的功等于物体B的动能增量与弹簧弹性势能增量之和