1、计算题  据报道，最近在太阳系外发现了首颗“宜居”行星，其质量约为地球质量的6.4倍，其半径r约为地球半径的2倍，假设有一艘飞船环绕该星球做匀速圆周运动，且飞行速度为v=8km/s。(地球的半径R=6400km ，地球表面的重力加速度g=10m/s2)求：
（1）该行星表面的重力加速度：
（2）飞船到该星球表面的距离。( 结果保留2位有效数字)

参考答案：解：（1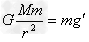）①
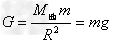②
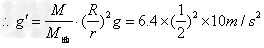=16m/s2 ③
（2）对飞船?⑤
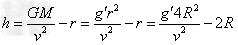=2.8×107m

本题解析：

本题难度：一般

2、计算题  “重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下：如图，P、Q为某地区水平地面上的两点，在P点正下方一球形区域内储藏有石油，假定区域周围岩石均匀分布，密度为；石油密度远小于，可将上述球形区域视为空腔。如果没有这一空腔，则该地区重力加速度（正常值）沿竖直方向；当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向（即PO方向）上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量，常利用P点附近重力加速度反常现象。已知引力常数为G。

（1）“重力探矿”利用了“割补法”原理：如图所示，在一个半径为R、质量为M的均匀球体中，紧贴球的边缘挖去一个半径为R/2的球形空穴后，剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
（2）设球形空腔体积为V，球心深度为d（远小于地球半径），=x，利用“割补法”原理：如果将近地表的球形空腔填满密度为的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值（在OP方向上的分量）
（3）若在水平地面上半径L的范围内发现：重力加速度反常值在与（k>1）（为常数）之间变化，且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的，试求此球形空腔球心的深度和空腔的体积。

参考答案：（1）；（2）；（3）；

本题解析：
试题分析:（1）把整个球体对质点的引力F看成是挖去的小球体对质点的引力F1和剩余部分对质点的引力F2之和，即F=F1+F2
填补上的空穴的完整球体对质点m的引力，挖去的半径为R/2的小球的质量，对质点m的引力
挖去剩余部分对质点m的引力
（2）（1）如果将近地表的球形空腔填满密度为ρ的岩石，则该地区重力加速度便回到正常值．因此，重力加速度反常可通过填充后的球形区域产生的附加引力①来计算，式中的m是Q点处某质点的质量，M是填充后球形区域的质量，M=ρV②．
而r是球形空腔中心O至Q点的距离，△g在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小．Q点处重力加速度改变的方向沿OQ方向，重力加速度反常△g′是这一改变在竖直方向上的投影，联立以上式子得
（3）由（2）结论可知：重力加速度反常△g′的最大值和最小值分别为
，，由题意重力加速度反常值在 与 （k>1）（ 为常数）之间变化可知：由题设有，
联立以上式子得，地下球形空腔球心的深度和空腔的体积分别为
；

本题难度：困难

3、简答题  一颗人造地球卫星在绕地球做匀速圆周运动，卫星距地面的高度是地球半径的15倍，即h=15R，试计算此卫星的线速度大小．已知地球半径R=6400km，地球表面重力加速度g=10m/s2．

参考答案：设地球质量为M，人造卫星质量为m，地面处一个物体质量为m′
对卫星，万有引力提供向心力：GMm(R+h)2=mv2R+h
对地面物体，重力等于万有引力：GMm′R2=m′g
联立二式解得：v=

本题解析：

本题难度：一般

4、选择题  按照我国月球探测活动计划，在第一步“绕月”工程圆满完成任务后，将开展第二步“落月”工程，预计在2013年前完成。假设月球半径为R，月球表面的重力加速度为g。。飞船沿距月球表面高度为3R的圆形轨道I运动，到达轨道的A点，点火变轨进入椭圆轨道Ⅱ，到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动。下列判断正确的是（   ）

A．飞船在轨道I上的运行速率
B．飞船在A点点火变轨的瞬间，动能增加
C．飞船在A点的线速度大于在B点的线速度
D．飞船在轨道Ⅲ绕月球运动一周所需的时间为