1、选择题  物体作自由落体运动，Ek表示其动能，Ep表示其势能，h表示其下落的距离，t、v分别表示其下落的时间和速度，以水平面为零势能面，下列图像中能正确反映各物理量之间关系的是 (? )??

参考答案：D

本题解析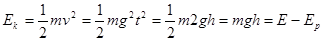：，根据关系式可知，动能与时间和速度都是非线性关系，跟重力势能是线性关系，跟下落高度成正比，选D

本题难度：简单

2、填空题  如图所示，一辆质量为1.5kg的小车静止在光滑水平面上，一个质量为0.50kg的木块，以2.0m/s的速度水平滑上小车，最后与小车以相同的速度运动．小车上表面水平，木块与车上表面的动摩擦因数是0.20．g取10m/s2，求
（1）木块与小车共同运动的速度的大小；
（2）木块在小车上相对滑行的时间；
（3）设小车与光滑水平面足够长，若水平面右端也有一高度与左端一样的平台，且小车与两边平台碰撞过程中均没有能量损失，求从木块滑上小车开始到木块与小车第n共同运动的时间及木块在小车上滑行的路程．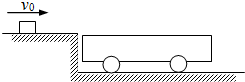

参考答案：（1）根据运动过程中动量守恒得：
mv0=（M+m）v1
解得：v1=mM+mv0=0.5m/s
（2）根据动量定理得：
μmgt=Mv1-0
t1=Mv0(M+m)μg=0.75s
（3）若M＞m，从第一次木板以v1反弹开始，有
Mv1-mv1=（M+m）v2
Mv2-mv2=（M+m）v3…
Mvn-1-mvn-1=（M+m）vn
解得：
v2=M-mM+mv1
v3=M-mM+mv2
…
vn=M-mM+mvn-1=(M-mM+m)n-1mM+mv0
根据动能定理得：
μmgx1=12mv02-12(M+m)v12
μmgx2=12mv12-12(M+m)v22
…
μmgxn=12mvn2-12(M+m)vn-12
解得：
x1=M2μg(M+m)v02
x2=2Mμg(M+m)v12
x3=2Mμg(M+m)v22=2Mμg(M+m)(M-mM+m)2v12

xn=2Mμg(M+m)vn-12=2Mμg(M+m)(M-mM+m)2(n-2)v12

x2，x3，x4，…xn是一个首项为2Mμg(M+m)v21
公比为(M-mM+m)2 的等比数列，共有n-1项
Sn=x1+2Mμg(M+m)v21n









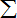
n=2(M-mM+m)2(n-2)
=x1+2Mμg(M+m)v21?1-(M-mM+m)2(n-1)1-(M-mM+m)2
=M2μg(M+m)v20+2Mμg(M+m)v21?1-(M-mM+m)2(n-1)1-(M-mM+m)2
=M2μg(M+m)v20+2Mμg(M+m)?(mM+m)2v20?1-(M-mM+m)2(n-1)1-(M-mM+m)2
=Mv202μg(M+m)+mv202μg(M+m)?[1-(M-mM+m)2(n-1)]
在板上滑行的时间（不包含从共速至与平台碰撞的时间）
-μmgt2=Mv2-Mv1
-μmgt3=Mv3-Mv2…
-μmgtn=Mvn-Mvn-1
t2=2Mμg(M+m)v1
t3=2Mμg(M+m)v2=2Mμg(M+m)?M-mM+mv1
tn=2Mμg(M+m)vn-1=tn=2Mμg(M+m)?(M-mM+m)n-2v1

t2，t3，t4，…tn是一个首项为2Mμg(M+m)v1 公比为 (M-mM+m) 的等比数列，共有n-1项
tn=t1+2Mμg(M+m)v1n









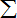
n=2(M-mM+m)n-2=t1+2Mμg(M+m)v1?1-(M-mM+m)(n-1)1-(M-mM+m)
=Mv0(M+m)μg+2Mμg(M+m)v1?1-(M-mM+m)(n-1)1-(M-mM+m)
=Mv0(M+m)μg+2Mμg(M+m)?mM+mv0?1-(M-mM+m)(n-1)1-(M-mM+m)
=Mv0μg(M+m)?[2-(M-mM+m)(n-1)]
同理可得：若M＜m，
x2，x3，x4，…xn是一个首项为 2Mμg(M+m)v21
公比为(m-Mm+M)2 的等比数列，
共有n-1项
Sn=x1+2Mμg(M+m)v21n









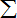
n=2(m-Mm+M)2(n-2)
=x1+2Mμg(M+m)v21n









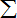
n=2(m-Mm+M)2(n-2)
=M2μg(M+m)v20+2Mμg(M+m)v21?1-(m-Mm+M)2(n-1)1-(m-Mm+M)2
=M2μg(M+m)v20+2Mμg(M+m)?(mM+m)2v20?1-(m-Mm+M)2(n-1)1-(m-Mm+M)2
=Mv202μg(M+m)+mv202μg(M+m)?[1-(m-Mm+M)2(n-1)]
在板上滑行的时间（不包含从共速至与平台碰撞的时间）
-μmgt2=mv2-mv1
-μmgt3=mv3-mv2
…
-μmgtn=mvn-mvn-1
t2=2mμg(m+M)?v1
t2=2mμg(m+M)?v2=2mμg(m+M)?m-Mm+Mv1
所以tn=2mμg(m+M)?vn-1=2mμg(m+M)?(m-Mm+M)n-2v1

t2，t3，t4，…tn是一个首项为2mμg(m+M)v1，公比为 (m-Mm+M) 的等比数列，共有n-1项
tn=t1+2mμg(m+M)v1n









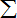
n=2(m-Mm+M)n-2=t1+2mμg(m+M)v1?1-(m-Mm+M)(n-1)1-(m-Mm+M)
=Mv0(M+m)μg+2mμg(m+M)v1?1-(m-Mm+M)(n-1)1-(m-Mm+M)
=Mv0(M+m)μg+2mμg(m+M)?mM+mv0?1-(m-Mm+M)(n-1)1-(m-Mm+M)
=Mv0(M+m)μg+m2v0μgM(m+M)?[1-(m-Mm+M)(n-1)]．
答：（1）木块与小车共同运动的速度的大小为0.5m/s；
（2）木块在小车上相对滑行的时间为0.75s；
（3）从木块滑上小车开始到木块与小车第n共同运动的时间为Mv0μg(M+m)?[2-(M-mM+m)(n-1)]或Mv0(M+m)μg+m2v0μgM(m+M)?[1-(m-Mm+M)(n-1)]，木块在小车上滑行的路程为Mv202μg(M+m)+mv202μg(M+m)?[1-(M-mM+m)2(n-1)]或Mv202μg(M+m)+mv202μg(M+m)?[1-(m-Mm+M)2(n-1)]．

本题解析：

本题难度：一般

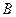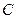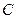3、选择题  物块一次沿轨道1从点由静止下滑至底端点，另一次沿轨道2从点由静止下滑经点至底端点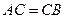，，如图所示。物块与两轨道的动摩擦因数相同，不考虑物块在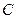点处撞击的因素，则在物块两次整个下滑过程中?（?）

A．沿轨道1下滑时的位移较小
B．沿轨道2下滑时的位移较小
C．物块滑至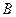点时速度大小相同
D．两种情况下损失的机械能相同

参考答案：CD

本题解析：略

本题难度：一般

4、计算题  如图所示，物块C质量mc=4kg，上表面光滑，左边有一立柱，放在光滑水平地面上。一轻弹簧左端与立柱连接，右端与物块B连接，mB=2kg；竖直放置的半径R=1.8m的光滑四分之一圆弧最低点的切线水平，且与物块C上表面在同一水平面上。物块A从圆弧的顶点静止释放，达到最低点时炸裂成质量m1=2kg，m2=1kg的两个物块1和2，物块1水平向左运动与B粘合在一起，物块2具有水平向右的速度，刚好回到圆弧的最高点。A、B都可以看着质点。取g="10" m/s2。求：

(1) 物块A炸裂时增加的机械能△E是多少？
(2) 在以后的过程中，弹簧最大的弹性势能Epm是多大？

参考答案：设物块A炸裂前的速度为v0，由动能定理
设物块1的初速度为v1，物块2的初速度为v2，则v2=v0
由动量守恒定律得mAv0= m1v1－m2v2
而mA=m1+m2，解得v1=12m/s
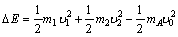，解得△E ="108" J
(2) 设物块1 与B粘合在一起的共同速度为vB，由动量守恒m1v1=(m1+mB)vB，所以vB="6" m/s
在以后的过程中，当物块C和1、B的速度相等时，弹簧的弹性势能最大，设共同速度为vm，由动量守恒? (m1+mB)vB = (m1+mB+mC)vm，有vm="3" m/s
由能量守恒得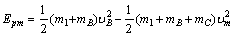，得Epm=" 36" J

本题解析：略

本题难度：简单

5、计算题  (6分)如图所示，光滑水平面上滑块A、C质量均为m=1kg，B质量为M=3kg。开始时A、B静止，现将C以初速度v0=2m/s的速度滑向A，与A碰后C的速度变为零，而后A向右运动与B发生碰撞并粘在一起。求：

①A与B碰撞后的共同速度大小；
②A与B碰撞过程中，A与B增加的内能。

参考答案：

本题解析：①对整个系统，根据动量守恒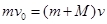---------（1分）
解得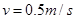---------------------------------------------------------（1分）
②对A和C由动量守恒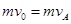---------------------------------（1分）
对A和B由能量守恒，
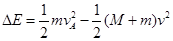---------------------------------------------（2分）
解得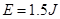-------------------------------------------------------------（1分）

本题难度：一般