1、计算题  如图所示，左侧为两间距d＝10 cm的平行金属板，加上电压；中间用虚线框表示的正三角形内存在垂直纸面向里的匀强磁场B1，三角形底点A与下金属板平齐，AB边的中点P恰好在上金属板的右端点；三角形区域AC右侧也存在垂直纸面向里，范围足够大的匀强磁场B2.现从左端沿中心轴线方向以v0射入一个重力不计的带电微粒，微粒质量m＝1.0×10－10 kg，带电荷量q＝1.0×10－4 C；带电粒子恰好从P点垂直AB边以速度v＝2×105 m/s进入磁场，则

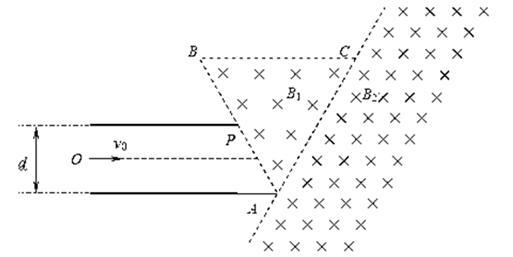
(1)求带电微粒的初速度v0；
(2)若带电微粒第一次垂直穿过AC，则求磁感应强度B1及第一次在B1中飞行时间；
(3)带电微粒再次经AC边回到磁场B1后，求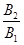的取值在什么范围可以使带电微粒只能从BC边穿出？

参考答案：(1) 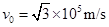?(2) ?(3)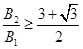

本题解析：(1)微粒在电场中做类平抛运动
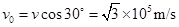?3分
(2)设带电微粒由P点垂直AB射入磁场，又垂直A C穿出，
所以作以A点为圆心的圆弧，设匀速圆周运动半径为R1，根据几何关系有
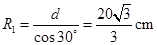? 2分
由，得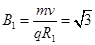T.? 2分
在磁场中飞行时间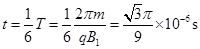? 2分
(3)再次经AC边回到磁场B1后不从AB边穿出就一定从BC边出磁场，所以当轨迹刚好与AB边相切时，设在B2中的半径为R2。如图所示

由几何关系：? 2分

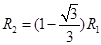
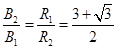? 3分
所以只需要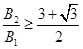即可? 2分

本题难度：一般

2、计算题  如图所示，两块水平放置、相距为d的长金属板接在电压可调的电源上。两板之间的右侧区域存在方向垂直纸面向里的匀强磁场。将喷墨打印机的喷口放置在两极板的正中央处，从喷口连续不断喷出质量均为m、水平速度大小均为v0、带电荷量为q的墨滴，调节电源电压，使墨滴在电场区域恰能沿中心线水平向右做匀速直线运动；进入电场和磁场共存区域后，最终打在上极板的P点，且速度方向与上极板成53°角。（sin53°=0.8,cos53°=0.6）。

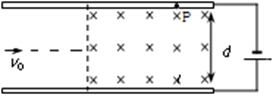
(1)判断墨滴所带电荷的种类，并求出两板间的电压；
(2)求磁感应强度B的值。

参考答案：(1)正电； ；(2)

本题解析：（1）墨滴在电场区域做匀速直线运动，有：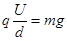
由①式得，．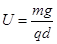
由于电场方向向上，电荷所受的电场力方向向上，可知墨滴带正电荷．
（2）墨滴垂直进入电磁场共存区域，重力仍与电场力平衡，合力等于洛伦兹力，墨滴做匀速圆周运动，有： 由图可知：

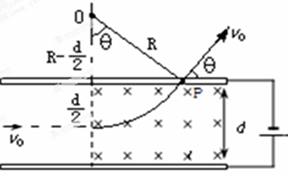
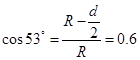．解得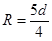
解得：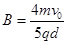
考点：带电粒子在匀强磁场中的运动.

本题难度：一般

3、简答题  如图所示，在xOy平面内，电荷量为q、质量为m的电子，从原点O垂直射入磁感应强度为B的匀强磁场中，电子的速度为v0，方向与x轴正方向成30°角，试求：
（1）电子从O点开始，第一次到达x轴所用的时间是多少？
（2）电子经过x轴的位置距坐标原点O的距离是多少？

参考答案：

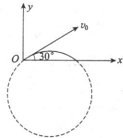
（1）电子在磁场中的运动轨迹如图中实线所示，占整个圆周的16，即其对应的圆心角为α=600
电子做匀速圆周运动的周期为T=2πmqB
所以电子第一次到达x轴所用的时间为?t=T6=πm3qB
（2）电子所受到的洛仑兹力提供它做匀速圆周运动的向心力，即qvB=mv20R
解得R=mv0qB
电子在x轴上的位置距原点的距离为x=R=mv0qB
答：（1）电子从O点开始，第一次到达x轴所用的时间是πm3qB；
（2）电子经过x轴的位置距坐标原点O的距离是mv0qB．

本题解析：

本题难度：一般

4、选择题  一个质量为m电荷量为q的带电粒子从x轴上的P(a，0)点以速度v，沿与x正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴射出第一象限。求匀强磁场的磁感应强度B=_________，射出点的坐标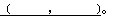

参考答案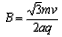：，（0，）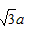

本题解析：

本题难度：一般

5、简答题  如图所示，在xOy平面内y>0的区域中存在垂直纸面向外的匀强磁场，磁感应强度大小为B0，在y<0的区域也存在垂直纸面向外的匀强磁场(图中未画出)，一带正电的粒子从y轴上的P点垂直磁场入射，速度方向与y轴正向成45?。粒子第一次进入y<0的区域时速度方向与x轴正向成135?，再次在y>0的区域运动时轨迹恰与y轴相切。已知OP的距离为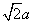，粒子的重力不计，求：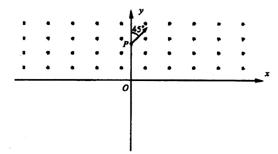
(1)y<0的区域内磁场的磁感应强度大小；
(2)粒子第2n(n∈N＋)次通过x轴时离O点的距离(本问只需写出结果)。

参考答案：
(1)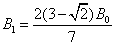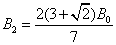，；(2) (n∈N＋)，(n∈N＋)

本题解析：
(1)当粒子通过y轴时速度方向沿y轴负方向时，粒子运动的轨迹如图1所示。

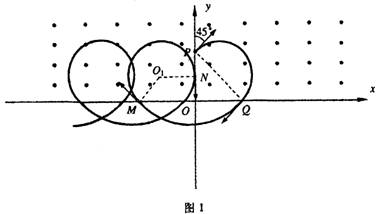
　　设粒子第一次、第二次通过x轴上的点为分别为Q、M，粒子在y>0和y<0区域作圆周运动的半径分别为R0和R1，通过y轴上的点为N，y<0区域的磁感应强度大小为B1
　　连接PQ，由题意知，　①(2分)
　　又有几何关系可得：PQ=2a②　(2分)
　　由①②式可得：R0=a　③(2分)
　　过M、N两点分别作该点速度方向的垂线，两垂线相交于O1点，O1即为粒子在y>0区域作圆周运动的圆心
　　由几何关系可得：
　　粒子在y<0区域内作圆周运动的弦长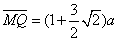
　　粒子在y<0区域内作圆周运动的半径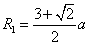　④(2分)
　　带电粒子在磁场中作圆厨运动的半径公式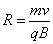　⑤(2分)
　　由③④⑤式可得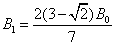：　⑥(2分)
　　当粒子通过y轴时速度方向沿y轴正向时，粒子运动的轨迹如图2所示。

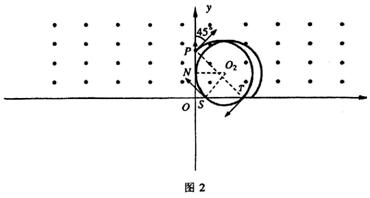
　　设粒子第一次、第二次通过x轴上的点为分别为T、S，粒子在y<0区域作圆周运动的半径为R2，y<0区域的磁感应强度大小为B2
　　由几何关系可以求得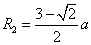：⑦(2分)
　　由③④⑦式可得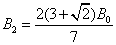：　⑧(2分)
　　(2)设粒子在两种情况下，第2n次通过x轴时离O点的距离分别为SI、SⅡ，当粒子通过y轴时速度方向沿y轴负向时，由几何关系可推算出：
　　(n∈N＋)⑨(2分)
　　当粒子通过y轴时速度方向沿y轴正向时，由几何关系可推算出：
　　(n∈N＋)⑩(2分)

本题难度：一般