1、计算题  如图所示，在y＜0的区域内存在匀强磁场，磁场方向垂直于xy平面并指向纸里，磁感应强度为B。一带负电的粒子（质量为m、电荷量为q，粒子所受重力不计）以速度v0从O点射入磁场，入射方向在xy平面内，与x轴正向的夹角为θ。求：
（1）该粒子射出磁场的位置；
（2）该粒子在磁场中运动的时间。?

参考答案：解：（1）设从A点射出磁场，O、A间的距离为L，射出时速度的大小仍为v，射出方向与x轴的夹角仍为θ，由洛伦兹力公式和牛顿定律可得：qv0B=m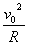
式中R为圆轨道半径，解得：R=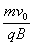?①
圆轨道的圆心位于OA的中垂线上，由几何关系可得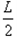：=Rsinθ?②
联解①②两式，得：L=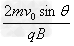
所以粒子离开磁场的位置坐标为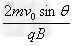（-，0）
（2）因为T==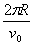
所以粒子在磁场中运动的时间，t＝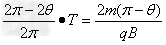

本题解析：

本题难度：一般

2、计算题  图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B。一带正电粒子从平板上狭缝O处以与平板成θ的初速度v射入磁场区域如图，最后到达平板上的P点。已知B、v以及P到O的距离l，不计重力，求此粒子的电荷量q与质量m之比。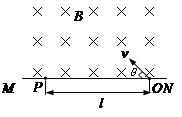

参考答案：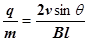 

本题解析：带电粒子从O点垂直射入磁场，在洛伦兹力作用下做匀速圆周运动．又从P点射出磁场，则PO连线就是运动圆弧的直径，由长度、运动速度及磁场可确定粒子的比荷．
解：（1）由左手定则可知：粒子带正电

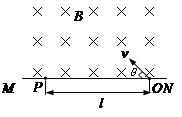
（2）粒子在磁场中做匀速圆周运动，设其半径为R ，
由几何关系可知：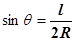
由洛伦兹力公式和牛顿第二定律，有
qvB=m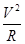
由此得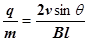  
考点：带电粒子在匀强磁场中的运动．
点评：将带电粒子的入射点与出射点连线，即为圆弧对应的弦．当圆心落在弦上，则弦就是直径．

本题难度：一般

3、简答题  空间存在垂直于纸面方向的均匀磁场其方向随时间作周期性变化，磁感应强度B随时间t变化的图线如图（甲）所示．规定B＞0时，磁场方向垂直纸面向外．现在磁场区域中建立一与磁场方向垂直的平面直角坐标系xoy，如图（乙）所示．一电量q=5π×10-7C质量m=5×10-10kg的带正电粒子，位于原点O处，在t=0时刻以初速度v0=πm/s沿x轴正方向开始运动，不计重力作用，不计磁场变化可能产生的一切其他影响．试求：

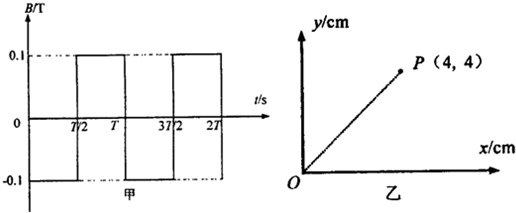
（1）带电粒子的运动半径；
（2）带电粒子从O点运动到P（4，4）点的最短时间；
（3）要使带电粒子过图中的P点，则磁场的变化周期T为多少？

参考答案：
（1）设粒子运动半径为R，则有
qvB=mv2R?
得：R=mvqB=0.01m
（2）设点电粒子的运动周期为T粒，则：
T粒=2πmqB=0.02s


?若磁场的变化周期T的12恰好为带电粒子运动周期T粒的14，即它的轨迹为4个14圆相连接，它的运动轨迹如图所示，此种情况带点粒子从O点运动到P点所用的时间最短，设为t，则：
t=T粒=0.02s
（3）要使带电粒子经过P点，则磁场变化的周期T和带电粒子在磁场中的运动周期T粒之间应满足的关系为：
T2=(n+14)T粒?
即：T=0.04×（n+14）s? n=0，1，2，3…
答：（1）带电粒子的运动半径为0.01m；
（2）带电粒子从O点运动到P（4，4）点的最短时间为0.02s
（3）要使带电粒子过图中的P点，则磁场的变化周期T为0.04×（n+14）s? n=0，1，2，3…

本题解析：

本题难度：一般

4、选择题  如图，在一水平放置的平板MN的上方有匀强磁场，磁感应强度的大小为B，磁场方向垂直于纸面向里。许多质量为m带电量为＋q的粒子，以相同的速率v沿位于纸面内的各个方向，由小孔O射入磁场区域。不计重力，不计粒子间的相互影响。下列图中阴影部分表示带电粒子可能经过的区域，其中R＝mv/Bq。哪个图是正确的

[? ]
A．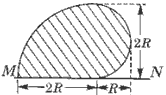
B．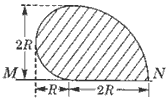
C．
D．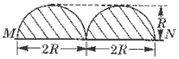

参考答案：A

本题解析：

本题难度：一般

5、选择题  如图所示，在x轴上方存在垂直于纸面向里的匀强磁场，磁感应强度为B．在xOy平面内，从原点O处沿与x轴正方向成θ角（0＜θ＜π）以速率v发射一个带正电的粒子（重力不计）．则下列说法正确的是（　　）
A．若θ一定，v越大，则粒子在磁场中运动的时间越短
B．若θ一定，v越大，则粒子在磁场中运动的角速度越大
C．若v一定，θ越大，则粒子在磁场中运动的时间越短
D．若v一定，θ越大，则粒子在离开磁场的位置距O点越远