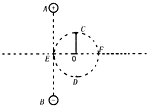
1、简答题  如图所示，将两个等量异种点电荷+Q和-Q分别固定于竖直线上的A、B两点，AB间距离为2d．EF为AB的中垂线．将质量为m、电荷量为+q（可视为质点且不影响原电场的分布）的带电小球固定在可绕O点自由转动的绝缘细杆的一端．从小球位于最高点C处由静止释放，已知OC=

参考答案：（1）等量异种电荷形成电场是中垂线两侧电场对称，中垂线上各点的场强与中垂线垂直，且中垂线是等势线，由C到F为研究过程，由动能定理得：
12mgd+qUCF=12mv2
解之得：UCF=mv2-mgd2q…①
（2）据等量异种电荷电场的对称性知：UCF=UFD…②
设小球到D点的速度为VD，由C到D为研究过程，动能定理得：mgd+qUCD=12mv2D…③
联立①②③解之得：VD=

本题解析：

本题难度：一般

2、选择题  一辆汽车以v1=6m/s的速度沿水平路面行驶时，急刹车后能滑行s1=3.6m，如果改以v2=8 m/s的速度行驶时，同样情况下急刹车后滑行的距离s2为
A.6.4 m
B.5.6 m
C.7.2 m
D.10.8 m

参考答案：A

本题解析：急刹车后，车只受摩擦力的作用，且两种情况下摩擦力大小是相同的，汽车的末速度皆为零.设摩擦力为F，根据动能定理得：-Fs1=0-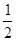mv12，-Fs2=0-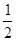mv22.两式相除得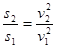：，故得汽车滑行距离s2=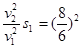×3.6 m=6.4 m.
思路分析：急刹车后，车只受摩擦力的作用，且两种情况下摩擦力大小是相同的，汽车的末速度皆为零.设摩擦力为F，根据动能定理分析
试题点评：本题考查了动能定理的应用

本题难度：一般

3、计算题  如图所示，在E=1×103N/C的竖直匀强电场中，有一光滑的半圆形绝缘轨道QPN竖直放置与一水平绝缘轨道MN相切连接，P为QN圆弧的中点，其半径R=40cm，一带负电电荷量q=10-4C的小滑块质量m=20g，与水平轨道间的动摩擦因数μ=0.4，从位于N点右侧s=1.5m处的M点以初速度v0向左运动，取g=10m/s2．

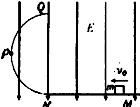
求：（1）若滑块初速度v0为6m/s, 则滑块通过P点时对轨道的压力是多大？
（2）若使小滑块在运动中不离开轨道QPN（Q点、N点除外）问小滑块从M点出发时的初速度满足什么条件？

参考答案：（1）1.3N（2）v0≥4m/s或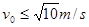

本题解析：（1）设小球到达P点时速度为v， 滑块从开始运动到达P点过程中，由动能定理得-mg?R+qE?R-μ（mg-qE）?S=1/2mv2—1/2 mv02?2分
代入数据解得：v2=24m/s? 1分
在P点，由支持力提供向心力，由向心力公式N=mv2/ R＝1.3N? 2分
由牛顿第三定律得到压力也为1.3N? 1分
故运动的滑块通过P点时对轨道的压力是1.3N
（2）设小球恰能到达Q点时速度为v，根据向心力公式，有mg-qE=mv2/ R ，
滑块从开始运动到达Q点过程中，由动能定理得
-mg?2R+qE?2R-μ（mg-qE）?S=1/2mv2—1/2 mv02? 2分
联立两式并代入数据解得：v0=4m/s? 1分
若滑块恰能滑到P点停止，滑块从开始运动到达P点过程中，由动能定理有
qE?R-mg?R-μ（mg-qE）?S="0—1/2" mv02? 2分
代入数据解得：v02=10m/s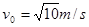，1分
综上所述，小滑块在运动中不离开轨道，小滑块从M点出发时的初速度必须满足：v0≥4m/s或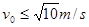2分
点评：在应用动能定理求解问题时，要明确两个状态一个过程，要进行受力分析和做功分析，本题又考查了圆周运动的知识，可见是一个综合性比较强的题目

本题难度：一般

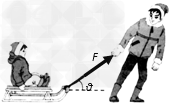
4、计算题  如图所示，已知小孩与雪橇的总质量为m=20 kg，静止于水平冰面上的A点，雪橇与冰面间的动摩擦因数为μ=0.1。（g取10m/s2）
（1）妈妈先用30N的水平恒力拉雪橇，经8秒到达B点，求A、B两点间的距离L。
（2）若妈妈用大小为30N，与水平方向成37°角的力斜向上拉雪橇，使雪橇从A处由静止开始运动并能到达（1）问中的B处，求拉力作用的最短距离。（已知cos37°=0.8 ，sin37°= 0.6）
（3）在第（2）问拉力作用最短距离对应的运动过程中，小孩与雪撬的最大动能为多少？?

参考答案：解：（1）对小孩进行受力分析，由牛顿第二定律得：
F-μmg=ma
a=0.5m/s2
L=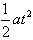
L=16?m
（2）设妈妈的力作用了x距离后撤去，小孩到达B点的速度恰好为0
方法一：由动能定理得Fcos37°x-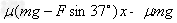（L?-x）=?0
方法二：Fcos37°-=ma1?
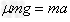2?


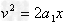
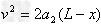
x=12.4?m
（3）小孩和雪撬在妈妈撤去力时的动能最大
方法一：由动能定理得Fcos37°x-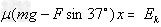
方法二：由动能公式得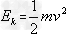
Ek=72J?(数值在71.9至72之间均可)

本题解析：

本题难度：一般

5、选择题  如图所示，光滑半球的半径为R，球心为O，固定在水平面上，其上方有一个光滑曲面轨道AB，高度为R/2．轨道底端水平并与半球顶端相切．质量为m的小球由A点静止滑下．小球在水平面上的落点为C（重力加速度为g）,则(? )

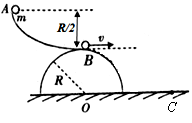
A．将沿半球表面做一段圆周运动后抛至C点
B．小球将从B点开始做平抛运动到达C点
C．OC之间的距离为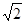R
D．小球从A运动到C的时间等于(1+)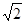

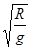
参考答案：BC

本题解析：如果小球在B点的速度足够大，则小球从B点开始做平抛运动，如果速度较小则会沿半球表面做一段圆周运动后抛至C点
A、小球在B开始做平抛运动的临界条件由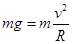得，小球从A点由静止滑到B点后，根据机械能守恒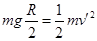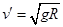，，因此小球从B点开始就做平抛运动，A选项错误
B、理由同A选项，B选项正确
C、小球从B点开始做平抛运动，由平抛运动规律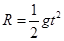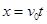，，可得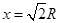，C选项正确
D、小球从B运动到C的时间由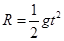可得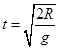，从A到B不是自由落体，时间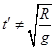，因此小球从A运动到C的时间不等于(1+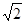)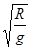，D选项错误
故选BC
点评：较难。判断小球是否沿球面运动的临界条件是，当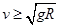时小球不沿球面下滑，当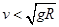时，沿球面下滑一段距离，当小球受到的支持力为零时开始离开斜面，做抛体运动。

本题难度：一般