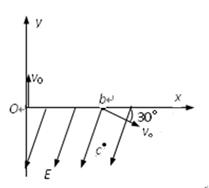
1、计算题 (12分)一质量为m、带电量为+q的粒子以速度v0从O点沿y轴正方向射入一圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强大小为大小为E,方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方c点,如图所示,已知 b到O的距离为L,粒子的重力不计,试求:
(1)磁感应强度B
(2)圆形匀强磁场区域的最小面积;
(3)c点到b点的距离
参考答案:(1) (2)
(2)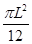 (3)
(3)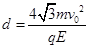
本题解析:(1)粒子在磁场中受洛仑兹力作用,作匀速圆周运动,设其半径为R,O点即进入磁场开始匀速圆周运动,粒子在磁场中的轨迹的圆心C必在x轴上,且b点速度切线x轴交点为b点,而b点不可能是圆心,所以b点在磁场区之外。过b沿速度方向作延长线,它与y轴相交于d点。
作圆弧过O点与y轴相切,并且与bd相切,切点a即粒子离开磁场区的地点。这样也求得圆弧轨迹的圆心C,如图所示。
由图中几何关系得:L=3R
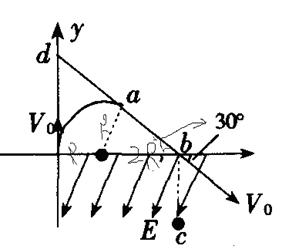
匀强磁场中洛伦兹力提供向心力即 ,得
,得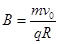
带入数据得?
(2)要使磁场的区域有最小面积,则线O 应为磁场区域的直径
应为磁场区域的直径

由几何关系知: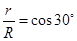
得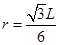 ?
?
∴匀强磁场的最小面积为: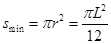
(3)带电粒子进入电场后,由于速度方向与电场力方向垂直,故做类平抛运动

设BC的距离为d,则由运动的合成知识有: ?
?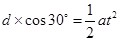
而
联立解得: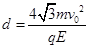
本题难度:一般
2、填空题 如图所示,水平放置的平行金属板A带正电,B带负电,A、B间距离为d,匀强电场的场强为E,匀强磁场的磁感应强度为B,方向垂直纸面向里,今有一带电粒子A、B间竖直平面内做半径为R的匀速圆运动,则带电粒子的转动方向为______时针方向,速率为______.

参考答案:由题意可知,粒子之所以能做匀速圆周运动,是因电场力与重力平衡,所以电场力竖直向上,根据电场线的方向,则粒子带负电,再根据左手定则可知,粒子沿着顺时针方向转动.
由洛伦兹力表达式有:
Bqv=mv2R ①
而在竖直方向上合力为零,则有:
qE=mg ②
联立①②解得:
v=gBRE.
故答案为:顺,gBRE.
本题解析:
本题难度:一般
3、选择题 在下图虚线所围的区域内,存在电场强度为E的匀强电场和磁感应强度为B的匀强磁场。已知从左方水平射入的电子,穿过该区域时并未发生偏转,假设重力忽略不计,则在该区域中的E和B的方向可能是

[? ]
A.E竖直向上,B垂直纸面向外
B.E竖直向上,B垂直纸面向里
C.E和B沿水平方向,并与电子运动的方向相同
D.E和B沿水平方向,并与电子运动的方向相反
参考答案:ACD
本题解析:
本题难度:一般
4、计算题 (15分)如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏离竖直方向的最大角度θ=74°。

⑴求电场强度的大小E;
⑵求小球向左摆动的过程中,对细线拉力的最大值;
⑶若从A点处释放小球时,给小球一个水平向左的初速度v0,则为保证小球在运动过程中,细线不会松弛,v0的大小应满足什么条件?
参考答案:⑴E= ;⑵T′=
;⑵T′= ;⑶v0≤
;⑶v0≤ 或v0≥
或v0≥
本题解析:⑴设小球最大摆角位置为C,在整个过程中,小球受重力mg、电场力qE和细线的拉力T作用,拉力T始终不做功,在小球由A运动至C的过程中,根据动能定理有:qElsinθ-mgl(1-cosθ)=0-0
解得:E= =
= =
=
⑵重力与电场力的合力大小为:F= =
= ?①
?①
其方向指向左下方,设与竖直方向成α角,根据几何关系有:tanα= =
= ,即α=37°?②
,即α=37°?②
当小球摆动至细线沿此方向,设为B位置时,小球对细线的拉力最大,则:T-F= ?③
?③
小球在由A运动至B的过程中,根据动能定理有:Fl(1-cosα)= -0?④
-0?④
根据牛顿第三定律可知,小球对细线的拉力为:T′=T?⑤
由①②③④⑤式联立解得:T′=
⑶要使细线不松弛有两种情况,当小球摆动过程中,细线的方向与F的方向不超过90°时,根据动能定理有:-Flcosα≤0-
解得:v0≤ ?⑥
?⑥
当小球能完成完整的圆周运动时,需满足:F≤ ?⑦
?⑦
根据动能定理有:-Fl(1+cosα)= -
- ?⑧
?⑧
由⑦⑧式联立解得:v0≥ ?⑨
?⑨
由⑥⑨式联立解得,为保证小球在运动过程中,细线不松弛,v0的大小应满足的条件为:v0≤ 或v0≥
或v0≥
本题难度:一般
5、计算题 如图所示,电阻忽略不计的、两根平行的光滑金属导轨竖直放置,其上端接一阻值为3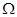 ?的定值电阻
?的定值电阻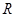 .在水平虚线
.在水平虚线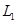 、
、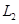 间有一与导轨所在平面垂直的匀强磁场
间有一与导轨所在平面垂直的匀强磁场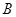 、磁场区域的高度为
、磁场区域的高度为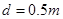 .导体棒
.导体棒 的质量
的质量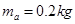 ,电阻
,电阻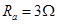 ;导体棒
;导体棒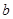 的质量
的质量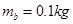 ,电阻
,电阻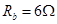 .它们分别从图中
.它们分别从图中 、
、 处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当
处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当 刚穿出磁场时
刚穿出磁场时 正好进入磁场.设重力加速度为g="10" m/s2.(不计
正好进入磁场.设重力加速度为g="10" m/s2.(不计 、
、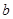 之间的作用,整个运动过程中
之间的作用,整个运动过程中 、
、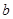 棒始终与金属导轨接触良好)
棒始终与金属导轨接触良好)

求:(1)在整个过程中 、
、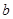 两棒克服安培力分别做的功;
两棒克服安培力分别做的功;
(2) 进入磁场的速度与
进入磁场的速度与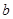 进入磁场的速度之比:
进入磁场的速度之比:
(3)分别求出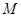 点和
点和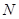 点距虚线
点距虚线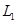 的高度.
的高度.
参考答案:(1)0.5J(2)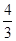 (3)0.75 m
(3)0.75 m
本题解析:本题中确定切割磁感线的那一部分导体相当于电源,根据题目中交代的运动情况写出牛顿第二定律的公式进行求解
(1)因a、b在磁场中匀速运动,其安培力等于各自的重力,由功的公式得
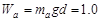 ?J
?J
 J
J
(2)b在磁场中匀速运动时:速度为vb,总电阻R1="7.5" Ω
b中的电流Ib= ? ①?
? ①?
 ? ②?
? ②?
同理,a棒在磁场中匀速运动时:速度为va,总电阻R2="5" Ω:
 ? ③?
? ③?
由以上各式得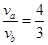 ? ④?
? ④?
(3)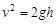 ? ⑤?
? ⑤?
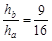 ? ⑥?
? ⑥?
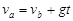 ? ⑦
? ⑦
 ? ⑧?
? ⑧?
由④⑤⑥⑦⑧得 m="1.33" m?
m="1.33" m?
 ?m="0.75" m
?m="0.75" m
本题难度:简单