1、填空题  一物体重20N，由静止开始匀加速下落，2s内下落19m，它下落的加速度的大小为______m/s2，空气对它的平均阻力是______N．

参考答案：物体做初速度为零的匀加速直线运动，根据位移时间关系公式，有：h=12at2，故a=2ht2=2×194=9.5m/s2；
物体受重力和阻力，根据牛顿第二定律，有：mg-f=ma；
故：f=m（g-a）=2×（10-9.5）=1N
故答案为：9.5，1．

本题解析：

本题难度：一般

2、选择题  一石块从高度为H处自由下落，当速度达到落地速度的一半时，它的下落距离等于
A．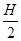
B．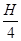
C．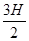
D．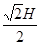

参考答案：B

本题解析：自由落体运动是初速度为零加速度为零g的匀加速直线运动，根据位移与速度关系公式求解．
设石块落地时的速度大小为v，由：v2-v02=2gx
得：v2-0=2gH…①
…②
由①②解得：?
故选B．
点评：本题考查应用自由落体运动规律解题的基本能力，是基本题，比较简单，考试时不能丢分．

本题难度：简单

3、简答题  
后来人们由此得出了重力势能EP（今天所说的重力势能）转换为动能EK的规律。离如今的41年前，有人根据爱因斯坦的思想，用光子作“落体”，在塔上做竖直下“抛”实验，发现在重力场中运动着的光子同样遵循③。
（1）已知光子的质量m=EK/c2=hγ/c2，如果从高度为H的塔顶竖直向下发射的光子频率为γ0，那么当光子到达塔底时，其频率γ变为多少？在此过程中，光子的颜色是向红端移动还是向紫端移动？
（2）如果从质量为M、半径为R的天体表面沿径向向外辐射出频率为γ0的光子，那么该光子到达无穷远处时频率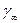变为多少？（提示：以无穷远处为零势能点，质量为m的质点在上述天体表面的引力势能为EP=-GMm/R）
（3）如果定义上述天体由万有引力造成的光子频率的红移量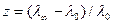，那么请写出天体质量与半径的比（M/R）跟引力红移（z）的关系式。
（4）已知太阳的引力红移z日=2×10-6，半径为R日；天狼星的伴星（一颗白矮星）的引力红移z=3×10-4，半径为R=0.0073R日。求这颗星的密度是太阳密度的多少倍？（要求小数点后仅保留一位有效数字）。

参考答案：
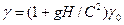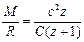(1)?光子的颜色向紫端移动(2)?(3) ?(4)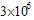

本题解析：（1）以塔底为零势面，根据能量守恒有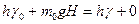：和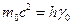
所以?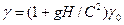
因为，所以光子的颜色向紫端移动。
（2）以无穷远为零势面，仍由能量守恒，
得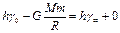：和
两式整理可求得：
（3）通过对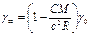
和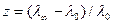
两式整理可求得：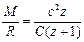
（4）因为Z日《Z《1，所以

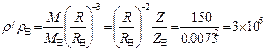
本题难度：一般

4、计算题  （12分）一个小球从某高处由静止开始下落，经过一个高2.05m的门口用了0.1s，忽略空气阻力，g=10m/s2，求小球的下落点离门口上缘的高度和小球经过门口过程的平均速度

参考答案：见试题分析

本题解析：设小球经过门口上下缘的速度分别为v1和v2 ,上缘离小球下落点的高度为H，则有：
?（2分）
v2 =v1 +gt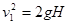?（2分）
?（2分）
V=h/t?（2分）
联合以上各式解得： H=20m?（2分）科.
V=20.5m/s?（2分）

本题难度：一般

5、计算题  一矿井深为125m，在矿井口每隔一定时间自由落下一小球，当第11个小球刚从矿井口下落时，第一个小球恰好到达井底，则：
（1）相邻小球开始下落的时间间隔为多少？
（2）这时第3个小球和第5个小球相距多远？

参考答案： （1）0.5s；（2）35m

本题解析：
试题分析: （1）设第一个小球下落到井底用时为t，根据自由落体运动位移时间关系
h＝gt2，则得 t=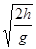=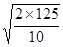s=5s
设相邻小球下落时间间隔为T，由题意知 t=10T，联立解得  来源:91考试网 91Exam.orgT=0.5s
（2）由以上计算可知，当第一个小球到达井底时第三个小球刚好下落t1=4s，第5个小球下落的时间为t2=3s 
故△H=H3-H5= g（t12-t22）=×10×（42-32）=35m
考点：自由落体运动

本题难度：困难