1、计算题  如图所示，真空中有以（r，0）为圆心，半径为r的圆形匀强磁场区域，磁感应强度为B，方向垂直纸面向里，在y= r的虚线上方足够大的范围内，有方向水平向左的匀强电场，电场强度为E，从O点向不同方向发射速率相同的质子，质子的运动轨迹均在纸面内，且质子在磁场中的偏转半径也为r，已知质子的电荷量为q，质量为m，不计重力、粒子间的相互作用力及阻力。求：

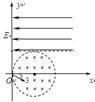
（1）质子射入磁场时速度的大小；
（2）沿x轴正方向射入磁场的质子，到达y轴所需的时间；
（3）与x轴正方向成30o角（如图中所示）射入的质子，到达y轴的位置坐标。

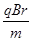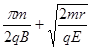参考答案：（1）（2）（3）（0，）

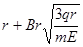本题解析：（1）质子射入磁场后做匀速圆周运动，有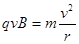?（2分） 得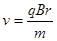?（1分）
（2）质子沿x轴正向射入磁场后经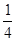圆弧后以速度v垂直于电场方向进入电场，在磁场中运动周期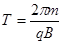?在磁场中运动的时间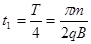?（2分）
进入电场后做类平抛运动，沿电场方向运动r后到达y轴，因此有
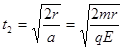?（1分）?所求时间为?（1分）
（3）质子在磁场中转过120o角后从P点垂直于电场线进入电场，如图所示。

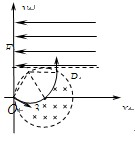
P点距y轴的距离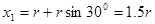（2分）其中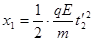（2分）
得质子到达y轴所需时间为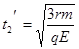?（1分）
在y方向质子做匀速直线运动，因此有
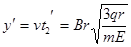?（1分）质子到达y轴的位置坐标为（0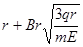，）（1分）
点评：处理方法不同：电场中粒子做类平抛运动，运用运动的合成与分解．在磁场中做匀速圆周运动，画轨迹，用牛顿定律和圆周运动知识处理．

本题难度：一般

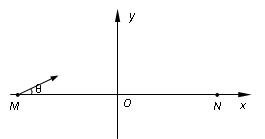
2、计算题  如图所示，在匀强电场中建立直角坐标系xoy，y轴竖直向上，一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线
运动,重力加速度为g。

（1）求匀强电场场强E的大小及方向；
（2）若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点，M、N两点关于原点o对称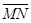，=L，微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B，方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。

参考答案：(1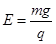）竖直向上(2）?

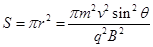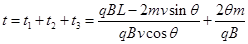
本题解析：
（1）当微粒在电场中做匀速直线运动时，它所爱的电场力与重力平衡。所以有：qE－mg=0?①（2分）
由①式可解得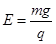：?②（1分）
E的方向竖直向上 （1分）
（2） 微粒在磁场中运动，由洛仑兹力和向心力公式得：
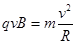?③（2分）
由③式得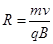：?④
如图所示，当PQ为圆形磁场的直径时，圆形磁场面积最小。（3分）

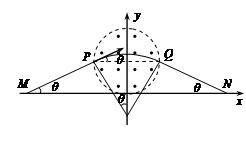
由几何知识可得：r=Rsinθ?⑤（2分）
其面积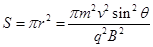?⑥
又由圆周运动规律可得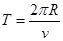：?⑦ （1分）
根据几何关系可知偏转角为2θ，则在磁场中运动的时间：
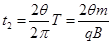?⑧（2分）
又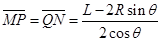?⑨（1分）
且有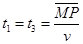?⑩（1分）
故微粒从M运动到N的时间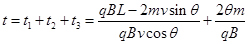：?（11） （2分）

本题难度：一般

3、计算题  在现代科技中，人们常常利用电场、磁场和重力场来控制带电微粒的运动。如图所示，直角坐标系位于竖直面内，y轴上的A点有一带正电的小球，小球的质量为m、电量为q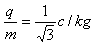，。若将小球从A点由静止释放，小球在场强为E1、方向平行于坐标平面的匀强电场和重力场的作用下沿直线做匀加速运动到X轴上的B点。在X轴的上方，小球在场强为E2、磁感应强度为B=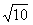T的磁场和重力场作用下做匀速圆周运动，轨迹是圆周的一部分，且关于y轴对称，已知A、B两点坐标分别为A（0，-l），B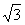（，0），g取10m／s2，求：
（1）场强E2的大小和方向；
（2）场强E1的大小和方向。（结果可以保留根式）

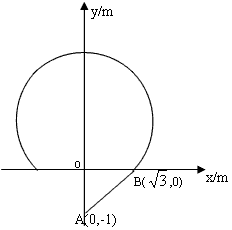
参考答案：解：（1）粒子在x轴上方做匀速圆周运动，所以洛伦兹力充当向心力，电场力和重力平衡

解得E2=10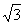N／C，方向竖直向上
（2）在△AOB中，∠ABO=30°，半径O1B与x轴成60°，所以Rcos60°=OB
解得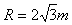
根据牛顿第二定律，粒子做圆周运动时有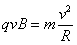
解得：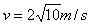
从A到B做匀加速直线运动，则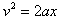
解得a=10m／s2
根据平行四边形定则，有
解得E1=30N／C，与x轴正方向成60°斜向上

本题解析：

本题难度：困难

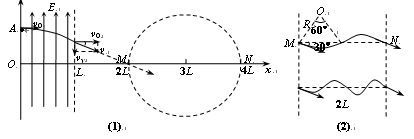
4、计算题   如图（甲）所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,右侧有一个以点(3L,0)为圆心、半径为L的圆形区域,圆形区域与x轴的交点分别为M、N。现有一质量为m、带电量为e的电子,从y轴上的A点以速度v0沿x轴正方向射入电场,飞出电场后从M点进入圆形区域,速度方向与x轴夹角为30°。此时在圆形区域加如图（乙）所示周期性变化的磁场,以垂直于纸面向外为磁场正方向）,最后电子运动一段时间后从N点飞出,速度方向与进入磁场时的速度方向相同（与x轴夹角也为30°）。求:

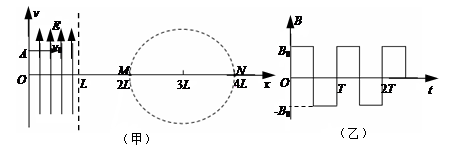
⑴ 电子进入圆形磁场区域时的速度大小；
⑵ 0≤x≤L区域内匀强电场场强E的大小；
⑶ 写出圆形磁场区域磁感应强度B0的大小、磁场变化周期T各应满足的表达式。

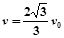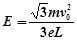参考答案：（1）（2）（3）

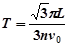
本题解析：本题考查带电粒子在复合场中的运动，难度较大，带电粒子先在匀强电场做类平抛运动，可以把出射速度分解后进行求解，出电场后带电粒子不受任何力的作用做匀速直线运动，可求出进入磁场时的速度方向，由磁场的可重复性可判断从N点射出时，带电粒子半径的表达式和周期表达式
⑴ 电子在电场中作类平抛运动,射出电场时,如图1所示.

由速度关系: ……2分?
解得?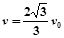…………2分
⑵ 由速度关系得…………2分
在竖直方向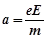…………1分?
…………1分
解得?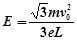…………2分
⑶在磁场变化的半个周期内粒子的偏转角为60°（如图2）,所以,在磁场变化的半个周期内,粒子在x轴方向上的位移恰好等于R。粒子到达N点而且速度符合要求的空间条件是: ?
…………2分?
电子在磁场作圆周运动，洛伦兹力提供向心力。
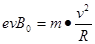………1分?
得?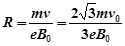……1分
解得， (n=1、2、3……) …………1分
若粒子在磁场变化的半个周期恰好转过1/6圆周,同时MN间运动时间是磁场变化周期的整数倍时,可使粒子到达N点并且速度满足题设要求。应满足的时间条件:
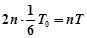…………1分?
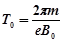…………1分
代入T的表达式得: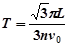(n=1、2、3……) …………1分

本题难度：一般

5、填空题  如图所示，光滑绝缘轨道ABP竖直放置，其轨道末端切线水平，在其右侧有一正交的匀强电场、磁场区域，电场竖直向上，磁场垂直纸面向里．一带电小球从轨道上的A点静止滑下，经P点进入场区后，恰好沿水平方向做直线运动．则
（1）小球做沿水平方向做______直线运动（选选填“匀速”，“匀变速”或“变加速”）．
（2）小球带______电（选填“正”或“负”）；
（3）若小球从B点由静止滑下，进入场区后将立即向______偏（选填“上”或“下”）．

参考答案：（1）带电小球进入场区沿水平方向做直线运动，直线运动的合力为零或者与速度共线，小球受的重力、电场力、洛伦兹力均沿着竖直方向，故合力为零，小球做匀速直线运动；
（2）若小球带负电，所受电场力、重力、洛伦兹力均竖直向下，小球受力不平衡，矛盾；
若小球带正电，所受电场力、洛伦兹力竖直向上，重力竖直向下，可以平衡；
故小球带正电荷；
（3）若小球从B点由静止滑下，根据机械能守恒定律可知，速度变小，则洛伦兹力也变小，导致重力大于洛伦兹力与电场力之和，所以进入场区后将立即向下偏；
故答案为：（1）匀速；（2）正；（3）下．

本题解析：

本题难度：一般