1、选择题  从同一高度处同时将完全相同的a、b两个小球分别竖直上抛和竖直下抛，它们的初速度大小也相同，以下说法中正确的是（不计空气阻力）（　　）
A．a、b两球触地瞬时的速度不同
B．在空中运动过程中，a、b两球的加速度相同
C．a、b两球运动的位移不同
D．a、b两球运动的路程相同

参考答案：A、两个小球从抛出到落地，只有重力做功，机械能守恒．因为两个小球完全相同，故m相同；又从同一高度以相同的初速度大小抛出，故h、V0相同．
? 根据12mV2+mgh=12mV2t知Vt相同．故A错误．?
B、在空中运动过程中，不计空气阻力，则只受重力作用，根据牛顿第二定律F=ma可知a=mgm=g，加速度相同．故B正确．
C、位移只与初末位置有关，同一高度处抛出到落地位移相同．故C错误．
D、路程则和运动轨迹有关，同一高度处竖直上抛的小球的运动路程要比竖直下抛小球的运动路程大．故D错误．
故选B．

本题解析：

本题难度：一般

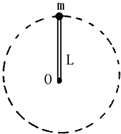
2、简答题  用长为L的轻质细杆拉着质量为m的小球在竖直平面内作圆周运动，小球运动到最高点时，速率等于2

参考答案：
（1）假设小球在最高时，所受杆的弹力方向竖直向下，由牛顿第二定律得
mg+F=mv2L，又v=2

本题解析：

本题难度：一般

3、简答题  如图，质量m、带电+q的小球套在绝缘杆上，杆与水平面成θ角，球杆间摩擦系数为μ，且有μsinθ＞cosθ，杆又放在竖直的平板AB之间，AB间距离为d，并和变阻器及电源相连，变阻器总电阻为R，电源内阻为r．求：
（1）当滑动触头P位于a点时，小球沿杆下滑的加速度为多少？当P由a滑向b时，小球加速度如何变化？
（2）若当P位于变阻器中间时，小球沿杆下滑的加速度恰好达到最大，求这最大加速度值及电源电动势值．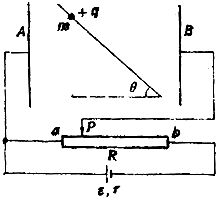

参考答案：（1）当滑动触头P位于a点时，电容器板间电压为零，板间无电场，小球不受电场力，由牛顿第二定律
得：mgsinθ-μmgcosθ=ma，得 a=g（sinθ-μθ）
当P由a滑向b时，小球受到水平向右的电场力，设为F．
开始阶段，Fsinθ＜mgcosθ，杆对球的弹力垂直杆向上，大小为N=mgcosθ-Fsinθ，小球的加速度为a=mgsinθ-μNm=gsinθ-μm（mgcosθ-Fsinθ），P由a滑向b时，F增大，则可知，加速度逐渐增大；后来阶段，Fsinθ＞mgcosθ，杆对球的弹力垂直杆向上，大小为N=Fsinθ-mgcosθ，小球的加速度为a=mgsinθ-μNm=gsinθ-μm（Fsinθ-mgcosθ），F增大时，a减小，所以当Fsinθ=mgcosθ时，加速度最大．故在整个过程中，小球的加速度先增大后减小．
（2）由上分析知，当Fsinθ=mgcosθ时，加速度最大为gsinθ．，而且有? F=mgcotθ．
又F=qUd，U=12?RR+rE
联立解得，电源的电动势E=2mgd(R+r)cotθqR
答：（1）当滑动触头P位于a点时，小球沿杆下滑的加速度为gsinθ．当P由a滑向b时，小球加速度先增大后减小．
（2）小球最大加速度值为gsinθ，电源电动势值为2mgd(R+r)cotθqR．

本题解析：

本题难度：一般

4、选择题  如图所示，两个质量分别为m1=2kg? m2=3kg的物体置于光滑的水平面上，中间用轻质弹簧秤连接。两个大小分别为F1=30N? F2=20N的水平拉力分别作用在m1? m2上，则

A．弹簧秤的示数是10N
B．弹簧秤的示数是50N
C．在突然撤去F2的瞬间，m1的加速度不变
D．在突然撤去F2的瞬间，m2的加速度不变

参考答案：C

本题解析：先整体分析得到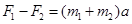，代入数据解得a=2m/s2,
设弹簧秤受到的拉力为F，再对m1受力分析得到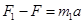，代入数据解得F=26N，所以弹簧秤的示数是26N，AB错；在突然撤去F2的瞬间，弹簧的弹力与撤去前相同，m1受力不变，即m1的加速度不变，C对；m2的合力增大，加速度增大，D错。
点评：学生明确弹簧秤的读数等于拉秤钩力的大小，能熟练运用整体法和隔离法去分析物体受力。

本题难度：一般

5、选择题  如图所示，质量均为m的A、B两球之间系着一条不计质量的轻弹簧，放在光滑的水平面上，A球紧靠墙壁，今用力F将B球向左推压弹簧，平衡后，突然将力F撤去的瞬间，则?（?）

A、A球的加速度大小为F/m ?B、A球的加速度为零
C、B球的加速度为零? D、B球的加速度大小为F/m

参考答案：BD

本题解析：用力F将B球向左推压弹簧，平衡后，弹簧弹力等于推力F，，撤去推力瞬间，B球受到弹簧的弹力不会突变，所以B球的加速度大小为a=F/m，D对；C错；在分析A球的受力，A受到的弹簧弹力和墙给的支持力等大反向，所以A的合力为零，加速度为零。A错，B对。

本题难度：简单