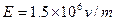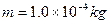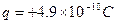1、简答题  已知如图，匀强电场方向水平向右，场强，丝线长L=40cm，上端系于O点，下端系质量为，带电量为的小球，将小球从最低点A由静止释放，求：

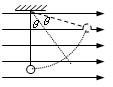
⑴小球摆到最高点时丝线与竖直方向的夹角多大？
⑵摆动过程中小球的最大速度是多大？

参考答案：74°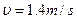　

本题解析：⑴这是个“歪摆”。由已知电场力Fe=0。75G摆动到平衡位置时丝线与竖直方向成37°角，因此最大摆角为74°。
⑵小球通过平衡位置时速度最大。由动能定理：?

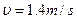
本题难度：简单

2、选择题  如图所示，质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间匀强电场中，P从两极板正中央射入，Q从下极板边缘处射入，它们最后打在同一点（重力不计），则从开始射入到打到上板的过程中（?）

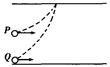
A．它们运动的时间
B．它们运动的加速度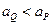
C．它们所带的电荷量之比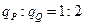
D．它们的动能增加量之比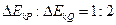

参考答案：C

本题解析：设P、Q两粒子的初速度是，加速度分别是和，粒子P到上极板的距离是，它们类平抛的水平距离为l。则对P，由，得到，同理对Q，，得到。同时可见，而，可见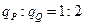。由动能定理，它们的动能增加量之比。综上，选C。

本题难度：一般

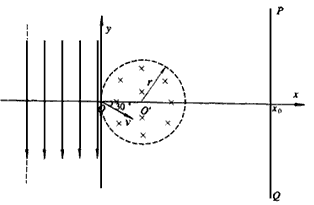
3、计算题  如图所示，xoy平面内，在轴左侧某区域内有一个方向竖直向下，水平宽度为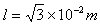，电场强度为的匀强电场。在y轴右侧有一个圆心位于x轴上，半径为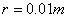的圆形磁场区域，磁场方向垂直纸面向里，磁感应强度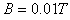，在坐标为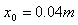处有一垂直于x轴的面积足够大的荧光屏PQ。今有一束带正电的粒子从电场左侧沿+x方向射入电场，穿出电场时恰好通过坐标原点，速度大小为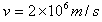，方向与x轴成30°角斜向下。若粒子的质量，电量为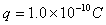，不计重力。试求：
（1）粒子射入电场时的位置坐标和初速度；
（2）若圆形磁场可沿x轴移动，圆心O"在x轴上的移动范围为，由于磁场位置的不同，导致该粒子打在荧光屏上的位置也不同，试求粒子打在荧光屏上的范围。

参考答案：解：（1）粒子沿+x方向进入电场后做类平抛运动，在O点将v沿x、y方向分解得
，
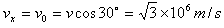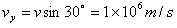
粒子在电场中做类平抛运动：





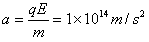
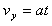
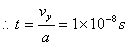
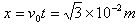
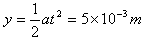
所以粒子射入电场时的坐标位置为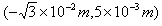
（2）洛仑兹力提供向心力，则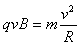

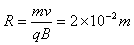
由几何关系知此时出射位置为D点，轨迹如图

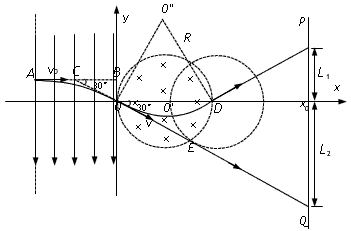
荧光屏最高端的纵坐标为：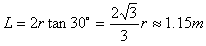
随着磁场向右移动荧光屏光点位置逐渐下移，当v方向与磁场圆形区域相切，此后，粒子将打在荧光屏的同一位置。其最低端的纵坐标为：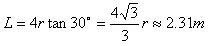

本题解析：

本题难度：困难

4、选择题  如图所示，在第二象限中有水平向右的匀强电场，电场强度为E，在第一象限内存在垂直纸面向外的匀强磁场，磁感应强度为B。有一重力不计的带电粒子以垂直于x轴的速度v0＝10 m/s从x轴上的P点进入匀强电场，恰好与y轴成45°角射出电场，再经过一段时间又恰好垂直于x轴进入第四象限。已知OP之间的距离为d＝0.5m，则关于带电粒子的下列说法不正确的是


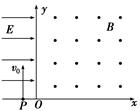
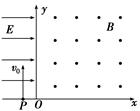
A．带正电荷
B．在电场中运动的时间为0.1 s
C．在磁场中做圆周运动的半径为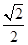m
D．在磁场中运动的时间为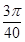s

参考答案：C

本题解析：粒子运动轨迹如图所示：

带电粒子在电场中向右偏转，可知粒子带正电，A正确；粒子在电场中做类平抛运动，设粒子在电场中运动的时间为t，则tanθ＝=1，tanα＝可知：tanθ=2tanα=2，由几何关系知：，则OC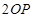＝=1m，粒子在垂直电场方向做匀速直线运动，则0.1s，B正确；由几何关系知：△OO`C为等腰直角三角形，则圆周运动的半径为，C错误；由类平抛运动规律知，进入磁场时的速度为v=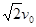，在磁场中运动的时间t`=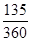= 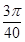s，D正确。
考点：本题考查带电粒子在复合场中的运动。

本题难度：一般

5、选择题  a、b、c三个相同带电粒子由同一点垂直场强方向进入偏转电场，其轨迹如图所示，其中b恰好飞出电场，由此可以肯定（?）

A．b和c同时飞离电场
B．进入电场时，c的速度最大，a的速度最小
C．动能的增量相比，a的最小，b和c的一样大
D．在b飞离电场的同时，a刚好打在负极板上

参考答案：BD

本题解析：带电粒子在电场中做类平抛运动，粒子在竖直方向上做匀加速直线运动，水平做匀速直线运动，因为三个带电粒子是相同的，故在电场中的加速度是相同的，根据结合图示可知，三个粒子在电场中的运动时间，所以可知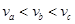，故A错误、B正确；带电粒子的动能增量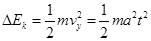，所以可知三个粒子的动能增量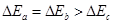，故C错误；因a、b粒子在电场中的运动时间相同，所以两粒子打在负极板与离开电场是同时的，所以D正确；

本题难度：一般