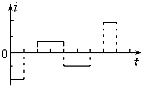
1、选择题 下列说法正确的是( )
A.线圈中电流恒定不变,自感电动势为零
B.线圈中电流恒定不变,自感电动势也不变
C.自感电动势的方向总是与原电流方向相反
D.自感电动势的方向总是与原电流方向相同
参考答案:A:根据法拉第电磁感应定律可知,线圈中电流恒定不变,通过线圈中的磁通量就不变,因此不产生感应电动势,所以A正确;
B:线圈中电流不变,线圈中的磁通量就不变,根据法拉第电磁感应定律可知,没有感应电动势,即自感电动势为零,而不是不变,所以B错误;
C:根据楞次定律可知,自感电动势的方向总是阻碍原电流的变化,即原电流增大时,自感电动势方向与原电流方向相反;原电流减小时,自感电动势方向与原电流方向相同,所以C错误;
D:由C项分析可知,若原电流增大,则自感电动势方向与原电流方向相反.D错误
故选:A
本题解析:
本题难度:简单
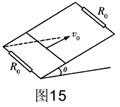
2、计算题 (16分)如图15所示,倾角为 °、电阻不计、间距L=0.3m且足够长的平行金属导轨处在磁感应强度B=1T、方向垂直于导轨平面的匀强磁场中。导轨两端各接一个阻值Ro=2
°、电阻不计、间距L=0.3m且足够长的平行金属导轨处在磁感应强度B=1T、方向垂直于导轨平面的匀强磁场中。导轨两端各接一个阻值Ro=2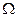 的电阻。在平行导轨间跨接一金属棒,金属棒质量m=1kg,电阻r=2
的电阻。在平行导轨间跨接一金属棒,金属棒质量m=1kg,电阻r=2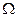 ,其与导轨间的动摩擦因数
,其与导轨间的动摩擦因数 =0.5。金属棒以平行于导轨向上的初速度
=0.5。金属棒以平行于导轨向上的初速度 =10m/s上滑直至上升到最高点的过程中,通过上端电阻的电荷量
=10m/s上滑直至上升到最高点的过程中,通过上端电阻的电荷量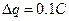 (sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
(1)金属棒的最大加速度
(2)上端电阻Ro中产生的热量
(3)金属棒上滑至最高点所用时间
参考答案:(1) /s2?
/s2?
(2)Q=5J
(3)Δt=0.994s
本题解析:(1)金属棒在上滑的过程中,回路的总电阻为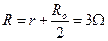 ?(1分)
?(1分)
对金属棒由牛顿第二定律得?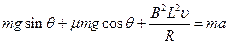 ?(2分)
?(2分)
金属棒上滑过程中的最大加速度对应的是金属棒的最大速度,金属棒上升过程做减速运动,所以金属棒上升过程中的最大加速度就是速度为 的瞬间,得:
的瞬间,得:
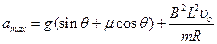 ?(2分)
?(2分)
代入数据后得最大加速度 /s2?(1分)
/s2?(1分)
(2)由题设条件可知:金属棒上升到最高点的过程中通过金属棒中的电荷量为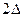 q,
q,
设金属棒中的平均电流为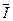 ,则
,则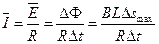 ?(2分)
?(2分)
又通过金属棒的电荷量: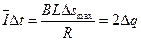 ?(*)?(1分);
?(*)?(1分);
设上端电阻产生的焦耳热为Q,则全电路产生的焦耳热为6Q,由能量守恒可知
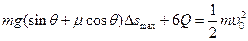 ?(2分);
?(2分);
联立以上各式,代入数据后? Q="5J?" (1分)
(3)设金属棒上滑至最高点所用时间为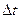 ,则
,则
由动量定理?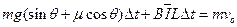 ?(3分);
?(3分);
联立(*)式,代入数据得 Δt="0.994s?" (1分)
本题难度:简单
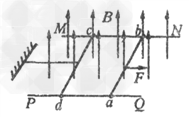
3、计算题 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中有两条光滑固定的平行金属导轨MN、PO,导轨足够长,间距为L,其电阻不计,导轨平面与磁场垂直,ab、cd为两根相同的、垂直于导轨水平放置的金属棒,电阻均为R,质量均为m,与金属导轨平行的水平细线一端固定,另一端与cd棒的中点连接,细线能承受的最大拉力为T,一开始细线处于伸直状态,ab棒在平行导轨的水平拉力的作用下以加速度a向右做匀加速直线运动,两根金属棒运动时始终与导轨接触良好且与导轨相垂直。?
(1)求经多长时间细线被拉断??
(2)求细线被拉断前,对ab棒的水平拉力随时间变化关系。?
(3)若在细线被拉断瞬间撤去水平拉力,求此后电路中产生的焦耳热。
参考答案:(1)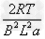
(2)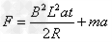
(3)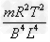
本题解析:
本题难度:困难
4、选择题 如图所示,ab、cd为两根水平放置且相互平行的金属轨道,相距L,左右两端各连接一个阻值均为R的定值电阻,轨道中央有一根质量为m的导体棒MN,其垂直放在两轨道上且与两轨道接触良好,棒及轨道的电阻不计。整个装置处于垂直于纸面向里的匀强磁场中,磁感应强度大小为B。棒MN在外驱动力作用下做简谐运动,其振动周期为T,振幅为A,通过中心位置时的速度为v0。则驱动力对棒做功的平均功率为( ? )
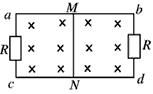
A.2mv02/T
B.B2L2V02/R
C.B2L2A2/8T2R
D.B2L2V02/2R
参考答案:B
本题解析:
本题难度:一般
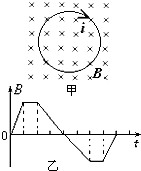
5、选择题 如图甲所示圆环形线圈处在匀强磁场B中,磁场方向与环面垂直.磁感应强度B随时间变化规律如图乙所示.规定图中所标的磁场方向和感应电流方向为正方向,则圆环中的感应电流i随时间变化的图中正确的是( )
A.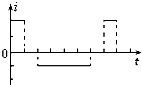
B.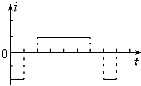
C.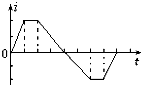
D.