1、简答题 在“验证机械能守恒定律”实验中,质量m=Ikg的重锤自由下落,在纸带上打出了一系列的点,如图所示,相邻点间的时间间隔为0.02s,长度单位是cm,g取9.8m/s2.从打下第一个点O到打下点B的过程中,重锤重力势能的减小量△Ep=______J,动能的增加量△Ek=______J.(计算结果保留三位有效数字)
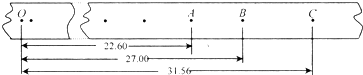
参考答案:(1)中间时刻的瞬时速度等于该过程中的平均速度来求B的速度大小:
vB=xAC2T=0.3156-0.22600.04=2.24m/s
动能的增加量△Ek=12mvB2=2.51J
重锤重力势能的减小量△Ep=mgh=2.65J
故答案为:2.65;2.51
本题解析:
本题难度:一般
2、计算题 要使一个小球着地后回跳的最大高度超过小球初位置高度5 m,必须用多大的初速度将它竖直上抛?(不计空气阻力以及球和地面碰撞时的机械能损失)
参考答案:解:设初速度为v0,抛出点的高度为h,由机械能守恒定律得
mgh+ mv02=mg(h+Δh)
mv02=mg(h+Δh)
所以v0= =
=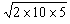 m/s=10 m/s
m/s=10 m/s
本题解析:
本题难度:一般
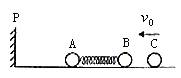
3、简答题 在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”。这类反应的前半部分过程和下述力学模型类似,两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态,在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图3.01所示,C与B发生碰撞并立即结成一个整体D,在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变,然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连,过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失),已知A、B、C三球的质量均为m。
(1)求弹簧长度刚被锁定后A球的速度。
(2)求在A球离开挡板P之后的运动过程中,弹簧的最大弹性势能
 ?
?
参考答案:(1)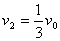
(2)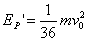
本题解析:(1)设C球与B球粘结成D时,D的速度为v1,由动量守恒得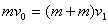 当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒得
当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒得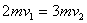 ,由以上两式求得A的速度
,由以上两式求得A的速度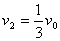 。
。
(2)设弹簧长度被锁定后,贮存在弹簧中的势能为EP,由能量守恒,有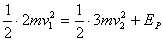 撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转弯成D的动能,设D的速度为v3,则有
撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转弯成D的动能,设D的速度为v3,则有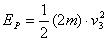
以后弹簧伸长,A球离开挡板P,并获得速度,当A、D的速度相等时,弹簧伸至最长,设此时的速度为v4,由动量守恒得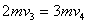
当弹簧伸到最长时,其势能最大,设此势能为EP",由能量守恒,有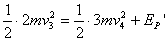 解以上各式得
解以上各式得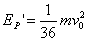 。
。
本题难度:简单
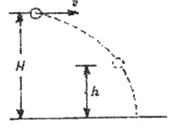
4、选择题 如图所示,从H高处以v平抛一小球,不计空气阻力,当小球距地面高度为h时,其动能恰好等于其势能,则(取地面为参考平面)
A.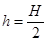
B.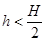
C.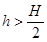
D.无法确定
参考答案:C
本题解析:
试卷分析:根据机械能守恒定律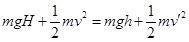 ,且
,且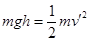 ,因此
,因此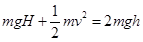 ,即
,即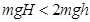 ,所以C答案正确。
,所以C答案正确。
点评:此类题型考察机械能守恒定律,并根据题目意思并结合不等式求解。
本题难度:简单
5、简答题 完成下列关于“验证机械能守恒定律”实验的有关问题:

(1)在验证机械能守恒定律时,如果以
为纵轴,以h为横轴,根据实验数据绘出的图线应是过坐标原点的直线就能验证机械能守恒定律,其斜率等于______.
(2)在做“验证机械能守恒定律”的实验时,用打点计时器打出纸带如图所示,其中A点为打下的第一个点,0、1、2…为连续的计数点.现测得两相邻计数点之间的距离分别为s1、s2、s3、s4、s5、s6,已知相邻计数点间的打点时间间隔均为T.根据纸带测量出的距离及打点的时间间隔,可以求出此实验过程中重锤下落运动的加速度大小表达式为______(逐差法),在打5号计数点时,纸带运动的瞬时速度大小的表达式为______.
参考答案:(1)物体下落时初速度为零,根据机械能守恒可知:mgh=12mv2,即v22=gh,故若以v22为纵轴,以h为横轴,图线是过原点的直线,其斜率大小等于重力加速度.
故答案为:重力加速度g.
(2)根据逐差法有:a1=s4-s13T2
a2=s5-s23T2
a3=s6-s33T2
a=a1+a2+a33=(s6+s5+s4-s3-s2-s1)9T2
根据匀变速直线运动的规律可知打5号计数点时速度大小为:
v5=s6+s52T
故答案为:(s6+s5+s4-s3-s2-s1)9T2,(s6+s5)2T.
本题解析:
本题难度:一般