1、选择题  如图所示，在第二象限内有水平向右的匀强电场，电场强度为E，在第一、第四象限内分别存在如图所示的匀强磁场，磁感应强度大小相等. 有一个带电粒子以初速度v0垂直x轴，从x轴上的P点进入匀强电场，恰好与y轴成45°角射出电场，再经过一段时间又恰好垂直于x轴进入下面的磁场.已知OP之间的距离为d，则带电粒子（?）

A．在电场中运动的时间为
B．在磁场中做圆周运动的半径为
C．自进入磁场至第二次经过x轴所用时间为
D．自进入电场至在磁场中第二次经过x轴的时间为

参考答案：AD

本题解析：
带电粒子在匀强电场中做类平抛运动，水平方向做匀加速直线运动，竖直方向做匀速直线运动，出电场时与y轴成45°角，则水平速度与竖直速度相等，则由水平方向，故A选项正确；竖直方向的位移：y=v0t=2d，带电粒子在匀强磁场中做匀速圆周运动，恰好垂直于x轴进入下面的磁场，如图所示，由几何关系可求出粒子的半径，所以B选项错误；由匀速圆周运动运动规律知,，解得，粒子垂直进入下面磁场中继续做匀速圆周运动，又垂直x轴出磁场，粒子自进入磁场至第二次经过x轴所用时间为，选项C选项错误，自进入电场至在磁场中第二次经过x轴的时间为，故选项D正确。本题的解题关键是画出运动的示意图。

本题难度：一般

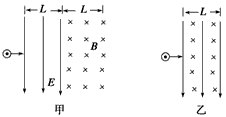
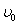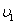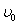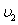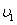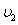2、选择题  一带电粒子以初速度沿垂直电场线的方向，先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场和匀强磁场，如图甲所示。电场和磁场对粒子做功为W1，粒子穿出磁场时的速度为；若把电场和磁场正交叠加，如图乙所示，粒子仍以初速度穿过叠加场区，电场和磁场对粒子做功为W2，粒子穿出磁场时的速度为。比较W1和W2、和的大小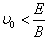（，不计重力）

[? ]
A．W1=W2、>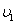
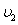
B．W1=W2、=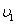
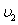
C．W1＜W2、＜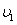
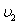
D．W1>W2、>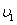

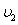
参考答案：D

本题解析：

本题难度：一般

3、简答题  如图所示，光滑绝缘的水平面上方，左边有垂直纸面向里的匀强磁场，右边有竖直向上的匀强电场。质量为m、带电量为q（正电）的小球a，以水平向右的初速度v沿水平面进入匀强磁场和匀强电场，恰好都不脱离水平面。在匀强电场中用绝缘细线悬挂一个质量也为m的不带电的小球b（可视为质点），小球处于静止且对水平面无压力。小球a进入匀强电场后与小球b正碰并粘在一起，恰好能绕悬挂点O在匀强电场中做竖直面内的圆周运动。若重力加速度为g，求：
（1）匀强磁场的磁感应强度B；
（2）匀强电场的电场强度E；
（3）绝缘细线的长度l。

参考答案：（1） ??（2） ?（3）

本题解析：（1）由于小球在磁场中运动时恰好不脱离水平面，由物体平衡条件有：
?
解得：?
（2）由于小球在电场中运动时恰好不脱离水平面，由物体平衡条件有：
?
解得：?
（3）a、b两个小球在最低点粘合在一起，根据动量守恒定律有：
? …………………①?
a、b两个小球粘合后在电场中、竖直面内做圆周运动，由牛顿第二定律和动能定理有：
? …………………②?
? …………………③?
联解①②③得：

本题难度：一般

4、计算题  如图所示，坐标系xoy在竖直平面内，空间有沿水平方向垂直于纸面向里的匀强磁场，磁感强度大小为B，在x<0的空间内还有沿x负方向的匀强电场．一个质量为m、带电量为q的油滴经图中M(-a，0)点(a>0)，沿着与水平方向成α角斜下作直线运向动，进入x>0区域，求：
(1)油滴带什么电荷?油滴做匀速直线运动还是匀变速直线运动?请说明理由；
(2)油滴在M点运动速度的大小；
(3)油滴进入x>O区域，若能到达x轴上的N点(在图9中未标出)，油滴在N点时速度大小是多少?

参考答案：（1）带正电?（2）

本题解析：（1）油滴受重力、洛伦兹力、电场力，做匀速直线运动，因为洛伦兹力始终与速度方向垂直，若速度发生变化，则大小发生变化，那么油滴就无法做直线运动，所以速度大小和方向均不变，即做匀速直线运动，则受力平衡，若油滴带正电，受向下的重力，垂直于运动方向斜向上的洛伦兹力，水平向左的电场力，可能平衡，若油滴带负电，则受水平向右的电场力和斜向下的洛伦兹力，不能使油滴平衡，所以油滴带正电
（2）根据平衡可知，竖直方向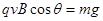：，即
(3)洛伦兹力不做功，所以油滴到N点有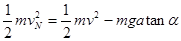：，则油滴在N点时速度大小为，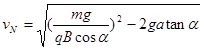

本题难度：简单

5、计算题  如图所示，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m、电荷量为q的带正电的粒子，从y轴上y＝h处的M点，以速度v0垂直于y轴射入电场，经x轴上x＝2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场。不计粒子重力。求：
（1）在原图上画出粒子在电场和磁场中运动轨迹示意图；
（2）电场强度大小E ；
（3）粒子在磁场中运动的轨道半径r；
（4）粒子从进入电场到离开磁场经历的总时间t。

参考答案：解：（1）粒子的运动轨迹如图所示 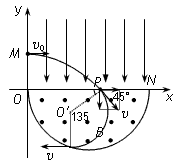（2）设粒子在电场中运动的时间为t1
x、y方向：2h＝v0t1，h＝at
根据牛顿第二定律：Eq＝ma
求出E＝
（3）根据动能定理：Eqh＝mv2－mv
将E的表达式代入上式，可求出v＝v0
再根据Bqv＝m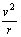，求出 r＝
（4）粒子在电场中运动的时间：t1＝
粒子在磁场中运动的周期：T＝＝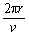
根据粒子入射磁场时与x轴成45°，射出磁场时垂直于y轴，可求出粒子在磁场中运动的圆弧所对的圆心角为135°
设粒子在磁场中运动的时间为t2＝T
求出t＝t1＋t2＝＋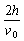

本题解析：

本题难度：困难