1、计算题 (2010·上海物理)(14分)如图,宽度L=0.5m的光滑金属框架MNPQ固定板个与水平面内,并处在磁感应强度大小B=0.4T,方向竖直向下的匀强磁场中,框架的电阻非均匀分布,将质量m=0.1kg,电阻可忽略的金属棒ab放置在框架上,并且框架接触良好,以P为坐标原点,PQ方向为x轴正方向建立坐标,金属棒从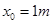 处以
处以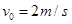 的初速度,沿x轴负方向做
的初速度,沿x轴负方向做 的匀减速直线运动,运动中金属棒仅受安培力作用。求:
的匀减速直线运动,运动中金属棒仅受安培力作用。求:

(1)金属棒ab运动0.5m,框架产生的焦耳热Q;
(2)框架中aNPb部分的电阻R随金属棒ab的位置x变化的函数关系;
(3)为求金属棒ab沿x轴负方向运动0.4s过程中通过ab的电量q,某同学解法为:先算出金属棒的运动距离s,以及0.4s时回路内的电阻R,然后代入
q=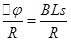

求解指出该同学解法的错误之处,并用正确的方法解出结果。
参考答案:(1)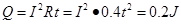 (2)
(2)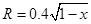 (3)见解析
(3)见解析
本题解析:(1)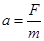 ,
,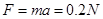
因为运动中金属棒仅受安培力作用,所以F=BIL
又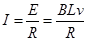 ,所以
,所以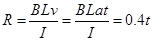
且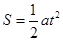 ,得
,得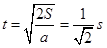
所以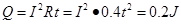
(2)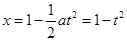 ,得
,得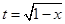 ,所以
,所以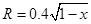 。
。
(3)错误之处:因框架的电阻非均匀分布,所求 是0.4s时回路内的电阻R,不是平均值。
是0.4s时回路内的电阻R,不是平均值。
正确解法:因电流不变,所以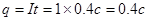 。
。
本题考查电磁感应、电路与牛顿定律、运动学公式的综合应用。难度:难。
本题难度:一般
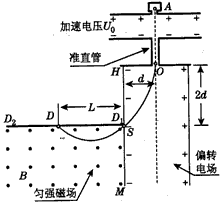
2、计算题 如图所示的装置可测离子的比荷(荷质比)。离子源A产生初速度可忽略不计的正离子,被电压为U0的加速电场加速后匀速通过准直管,然后从O点垂直射入匀强偏转电场,能正好从HM极板上的小孔S射出,立即进入垂直纸面向外的磁感应强度为B的匀强磁场区,最后打在水平放置的底片D1D2的D点(底片右端D1紧靠小孔S)。已知HO=d,HS=2d,DS=L,忽略粒子所受重力,试求:
(1)偏转电场场强E的大小;
(2)离子的比荷。
参考答案:解:(1)在加速电场中,根据动能定理:
在偏转电场中:横向位移
运动时间
加速度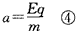
由①②③④得
(2)离开偏转电场时,横向速度
速度偏向角的正切
由②③⑥⑦得
离开偏转电场时速度
在磁场中,由几何知识得圆运动半径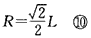
洛伦兹力提供向心力
由⑨⑩ 得粒子的比荷
得粒子的比荷
本题解析:
本题难度:困难
3、计算题 如图是一种测量血管中血流速度的仪器的示意图,在动脉两侧分别安装电极并加磁场,电极的连线与磁场方向垂直.设血管的直径为2 mm,磁场的磁感应强度为0.08 T,测得两极间的电压为0.10 mV,则血流速度为多少?

参考答案:解:血液中有大量的正、负离子,当血液流动时,血液中的正、负离子受到相反方向的洛伦兹力,使血管的上、下壁出现等量的异种电荷,使血管内形成一个竖直方向的电场,这样,正、负离子同时受到一个电场力的作用.当离子受到的电场力与洛伦兹力平衡时,血液上、下壁间形成一个稳定电场,血液在血管中稳定流动,设流速为v ,则:
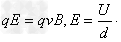
故: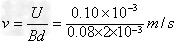 =0. 625 m/s
=0. 625 m/s
本题解析:
本题难度:一般
4、计算题 在图甲所示的装置中,粒子源A产生的初速度为零、比荷为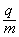 的正粒子沿轴线进入一系列共轴且长度依次增加的金属圆筒,奇数和偶数筒分别连接在图乙所示的周期为T、最大值为U0的矩形波电源两端,t=0时刻粒子进入第一个电场加速,粒子在每个筒内做匀速直线运动的时间等于
的正粒子沿轴线进入一系列共轴且长度依次增加的金属圆筒,奇数和偶数筒分别连接在图乙所示的周期为T、最大值为U0的矩形波电源两端,t=0时刻粒子进入第一个电场加速,粒子在每个筒内做匀速直线运动的时间等于 T,在相邻两筒之间被电场加速(加速时间不计)。粒子离开最后一个圆筒后垂直于竖直边界OE进入磁感应强度为B的匀强磁场,最后从OF边射出。(不计粒子所受重力)
T,在相邻两筒之间被电场加速(加速时间不计)。粒子离开最后一个圆筒后垂直于竖直边界OE进入磁感应强度为B的匀强磁场,最后从OF边射出。(不计粒子所受重力)
(1)求粒子在第n个筒内的速率及第n个筒的长度;
(2)若有N个金属筒,求粒子在磁场中做圆周运动的半径;
(3)若比荷为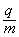 的粒子垂直于OF边射出,要使比荷为
的粒子垂直于OF边射出,要使比荷为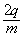 的粒子也能垂直于OF边从同一点S以相同速度射出,求 此时所加电源电压最大值U"以及磁感应强度的大小B"。
的粒子也能垂直于OF边从同一点S以相同速度射出,求 此时所加电源电压最大值U"以及磁感应强度的大小B"。


参考答案:解:
(1)设粒子在第n个筒内的速度为vn,根据动能定理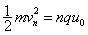 解得
解得
设第n个筒的长度为Ln,Ln=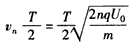 ;
;
(2)设粒子在磁场中做圆周运动的半径为R,根据
有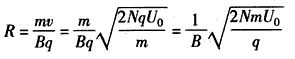 ;
;
(3)要使比荷为 的粒子加速后也获得vN的速度,设比荷为
的粒子加速后也获得vN的速度,设比荷为 的粒子的加速电压为U"
的粒子的加速电压为U"
则
解得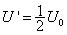
设比荷为 的粒子在磁场中做圆周运动的半径为R",要使比荷为
的粒子在磁场中做圆周运动的半径为R",要使比荷为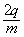 的粒子在磁场中同样在S点射出有
的粒子在磁场中同样在S点射出有
 解得
解得 。
。
本题解析:
本题难度:困难
5、简答题 如图所示,在xoy平面第Ⅰ象限有匀强电场,场强大小未知,其方向沿y轴正向;在第Ⅱ象限有垂直纸面向里的匀强磁场,磁感应强度为B;P处有一放射源,内装放射性物质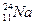 ,发生衰变生成新核
,发生衰变生成新核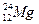 ,放出一个质量为m,电荷量为-q的带电粒子。带电粒子从P孔以初速度v0沿垂直于磁场方向进入匀强磁场中,初速度方向与-x轴的夹角θ=60°,粒子恰好从C孔垂直于y轴射入匀强电场,最后打在Q点,已知OQ=2OC,不计粒子的重力,
,放出一个质量为m,电荷量为-q的带电粒子。带电粒子从P孔以初速度v0沿垂直于磁场方向进入匀强磁场中,初速度方向与-x轴的夹角θ=60°,粒子恰好从C孔垂直于y轴射入匀强电场,最后打在Q点,已知OQ=2OC,不计粒子的重力,
(1)写出发生衰变时的核反应方程
(2)求粒子从P运动到Q所用的时间t
(3)求粒子到达Q点的动能EkQ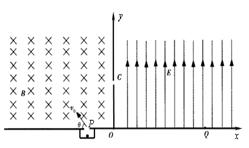
参考答案:(1)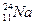 →
→ +
+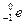 (2)(3+
(2)(3+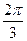 )
) (3)EKQ=mv02
(3)EKQ=mv02
本题解析:(1)放射性物质发生衰变的核反应方程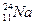 →
→ +
+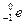 (3分)
(3分)
(2)设带电粒子在磁场中做匀速圆周运动的半径为R,由圆周运动知识得:
qv0B=m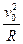 ? R=
? R=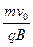 ①
①
由几何关系得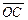 =R+Rcosθ ②
=R+Rcosθ ②
带电粒子在磁场中运动的时间t1=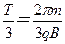 ?
? ③
③
带电粒子在电场中做类平抛运动, =2
=2 =v0t2,
=v0t2,
带电粒子在电场中运动的时间t2=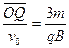 ④
④
粒子由P运动到Q的时间t=t1+t2=(3+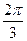 )
) ⑤
⑤
(3)设电场强度为E,粒子在电场中沿电场方向做匀加速直线运动
由S=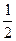 at2得?
at2得? =
=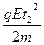 ,解得:E=
,解得:E= ⑥
⑥
根据动能定理,粒子到达Q点时的动能EKQ:
qE· =EKQ-
=EKQ-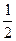 mv02 EKQ=mv02 ⑦
mv02 EKQ=mv02 ⑦
第①~⑥式各2分,第⑦式3分。
本题难度:一般