1、计算题  如图所示，半径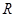=1.25m的l/4光滑圆弧轨道竖直固定，其末端切线水平，并与水平传送带相连，已知小滑块的质量为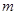=0.5kg，滑块与传送带间的动摩擦因数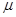=0.1，传送带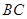长度为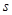=1.5m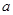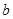，、两轮半径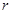=0.4m，当传送带静止时，用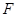="4" N的水平拉力将滑块从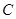端由静止开始向左拉动。取10m/s2。

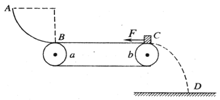
(1)若滑块到达端时撤去拉力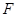，求：滑块沿弧形槽上升的最大高度；
(2)问题(1)中的滑块，从高点沿弧形槽再滑回端时，轨道对滑块的支持力多大?
(3)若拉力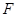作用一段距离后撤去，滑块到达光滑曲面某一高度而下滑时，以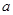、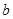两轮以角速度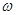=15rad/s顺时针转动，为使滑块能在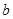轮最高点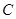离开传送带飞出，则拉力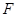作用的最短距离需多大?

参考答案：（1）h=1.05m（2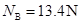）（3）

本题解析：（1）根据动能定理有?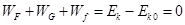
即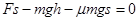：，代入数值解得h="1.05m"
（2）从高点滑回B点过程中，根据机械能守恒定律有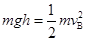
在B点有，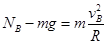
解以上两式得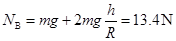
（3）根据题意，滑块要从b轮最高点C离开传送带飞出，则滑块运动至C点的速度最小为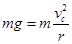，即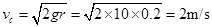
由于传送带的速度v带=rω=6m/s，滑块在B点的速度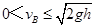，要使滑块从C点以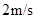飞出，可分析，滑块在传送带上从B到C做匀加速运动。根据牛顿第二定律，可得加速度

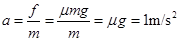
为了使滑块运动到C点时速度大于2m/s，则B点的速度最小为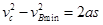：，代入数据可得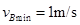
设拉力F作用的最短距离为x，则根据动能定理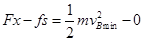
代入数据可以求得
点评：本题主要考察了动能定理及运动学基本公式的应用，要求同学们能正确分析物体的运动情况．

本题难度：一般

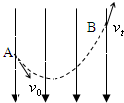
2、简答题  如图所示，质量为m?的滑块距挡板P的距离为?s0，滑块以初速度?v0沿倾角为θ的斜面上滑，滑块与斜面间的动摩擦因数为μ，斜面足够长，滑块所受摩擦力小于重力沿斜面向下的分力．若滑块每次与挡板相碰均无机械能损失，求滑块经过的总路程．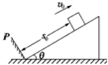

参考答案：滑块最终停在斜面底部，设滑块经过的总路程为s，
取斜面底边所在的水平面为零势能面
根据能量守恒定律，滑块的机械能全部转化为内能：
? E内=12mv?20+mgs0sinθ
滑块克服摩擦力所做的功：W=μmgscosθ?
对滑块运动的全过程应用功能关系：W=E内
解得：s=1μ（v202gcosθ+s0tanθ）
答：滑块经过的总路程为1μ（v202gcosθ+s0tanθ）．

本题解析：

本题难度：一般

3、选择题  一带电粒子（重力不计）沿图中虚线穿过一匀强电场，则粒子由A处到B处的过程中一定是（　　）
A．电势能逐渐减小
B．动能逐渐减小
C．该粒子带负电
D．电势能和动能之和不变