1、选择题  两物体质量之比为1:2，它们的初动能之比为1:3，它们与水平路面的动摩擦因数之比为3:2。则它们在水平路面上滑行的最大距离之比为
A．1:4　　? B．4:9　? C．1:9　? D．9:4

参考答案：B

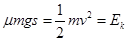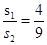本题解析：根据动能定理可得，即，所以,B正确，
故选B
点评：基础题，在计算的时候需要细心，

本题难度：简单

2、计算题  （ 12分）如图所示，AB为水平轨道，A、B间距离s=1m，BCD是半径为R=0.2m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点，整个轨道处于竖直向下的匀强电场中，场强大小为E=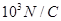。一带正电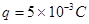的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s2)

（1）撤去F时小物块的速度大小；
（2）在半圆形轨道上小物块克服摩擦力做的功。

参考答案：（1）v=6m/s?
（2）4J

本题解析：（1）物体从A运动到B，根据动能定理可得：
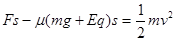?（3分）?
求得：v=6m/s?（1分）
（2）物体恰好能到达D点，此时轨道的压力为零，则：
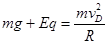?1?（3分）
物体从B点运动到D点，根据动能定理可得：
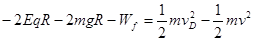?2?（3分）
联立1、2可得：Wf = 4J?（2分）
本题考查动能定理和圆周运动规律的应用，由A到B应用动能定理求得在B点速度大小，物体恰好通过D点，说明只有重力和电场力的合力提供向心力，由此求得D点速度大小，物体有B点到D点，根据动能定理可求得阻力做功大小，主要是通过受力分析确定过程中各力做功的正负，初末状态动能大小

本题难度：一般

3、计算题  （14分）如图所示，A、B为两块平行金属板，A板带正电、B板带负电。两板之间存在着匀强电场，两板间距为d、电势差为U，在B板上开有两个间距为L的小孔。C、D为两块同心半圆形金属板，圆心都在贴近B板的处，C板带正电、D板带负电。两板间的距离很近，两板末端的中心线正对着B板上的小孔，两板间的电场强度可认为大小处处相等，方向都指向。半圆形金属板两端与B板的间隙可忽略不计。现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒（微粒的重力不计）。试问：

⑴微粒穿过B板小孔时的速度为多大？
⑵为了使微粒能在CD板间运动而不碰板，CD板间的电场强度应为多大？
⑶从释放微粒开始计时，经过多长时间微粒通过半圆形金属板间的最低点P点？

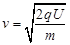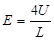参考答案：（1）（2）（3），

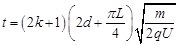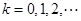
本题解析：⑴设微粒穿过B板小孔时的速度为v，根据动能定理，有
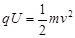?解得??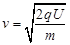
⑵微粒进入半圆形金属板后，电场力提供向心力，有
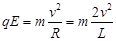?联立⑴、⑵，得?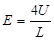
⑶微粒从释放开始经t1射出B板的小孔，则
?
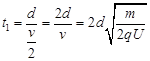设微粒在半圆形金属板间运动经过t2第一次到达最低点P点，则
?
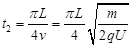所以从释放微粒开始，经过微粒第一次到达P点；
根据运动的对称性，易知再经过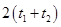微粒再一次经过P点；
所以经过时间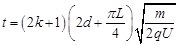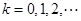，时微粒经过P点。
点评：本题考察了动能定理、并且巧妙的设计了靠电场力提供向心力。通过运动对称性得知粒子有多次回到P点的可能，从而分析本题的多解可能。

本题难度：一般

4、选择题  如图所示，一平直传送带以速度v=6m/s匀速运行，传送带把A处的工件运送到B处，已知A与B相距L=10m，若从A处把工件无初速地放在传送带上，工件与传送带之间的动摩擦因数为μ=0.2，将一质量m=1kg的工件从A传送到B过程中摩擦力对工件做的功（　　）（g取10m/s2）
A．6J
B．12J
C．18J
D．20J