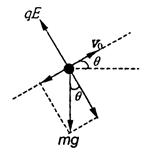
1、计算题 如图所示,K与虚线MN之间是加速电场,虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行,电场和磁场的方向如图所示,图中A点与O点的连线垂直于荧光屏.一带正电的粒子从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U=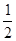 Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=
Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0= .若题中只有偏转电场的宽度d为已知量。
.若题中只有偏转电场的宽度d为已知量。
(1)画出带电粒子轨迹示意图。
(2)磁场的宽度L为多少?
(3)带电粒子在电场和磁场中垂直于v0方 向的偏转距离分别是多少?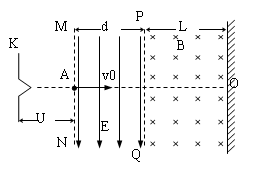
参考答案: (1)轨迹如图所示;(2)L= d;(3)0.914d
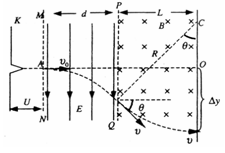
本题解析:
试题分析: (1)轨迹如图所示。
(2)粒子在加速电场中,由动能定理有 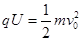
粒子在匀强电场中做类平抛运动,设偏转角为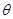 ,有
,有


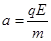
 U=
U=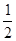 Ed
Ed
解得:θ=45º
由几何关系得,带电粒子离开偏转电场速度为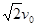
粒子在磁场中运动,由牛顿第二定律有:qvB=m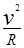
在磁场中偏转的半径为 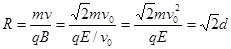
由图可知,磁场宽度L=Rsinθ="d"
(3)由几何关系可得:
带电粒子在偏转电场中距离为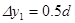 ,
,
在磁场中偏转距离为

粒子在电场、磁场中偏转的总距离为△y=△y1+△y2=0.914d
考点:动能定理的应用;运动的合成和分 91ExAm.org解.
本题难度:困难
2、简答题 一个带电粒子以初速度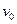 与水平方向成q 角(sinq =0.6)斜向上射入某匀强电场区域,粒子进入电场区域后沿直线运动.已知:粒子的质量为m=7.5×
与水平方向成q 角(sinq =0.6)斜向上射入某匀强电场区域,粒子进入电场区域后沿直线运动.已知:粒子的质量为m=7.5×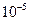 kg,带电量q=4×
kg,带电量q=4× C,取
C,取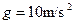 ,带电粒子所受的重力不能忽略.
,带电粒子所受的重力不能忽略.
(1)要使带电粒子进入电场后沿直线运动,求:该电场电场强度的最小值及方向.
(2)当电场强度为最小值时,通过计算说明该粒子进入这个电场区域后运动的性质.
?
参考答案:(1)1.5×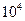 N/C 方向:垂直于
N/C 方向:垂直于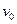 斜向上.(2)
斜向上.(2)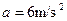
本题解析:(1)带电粒子受重力和电场力如图所示. (2分)
要使带电粒子沿直线运动,其初速度方向必与合外力方向共线,必须使粒子在垂直于运动直线方向上所受合力为零.要使电场强度最小,匀强电场方向应垂直于运动直线(或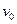 )向上,即:使电场力与重力在垂直于运动直线方向上的分力互相平衡. (2分)
)向上,即:使电场力与重力在垂直于运动直线方向上的分力互相平衡. (2分)
设E为满足条件的电场强度的最小值并满足方程:
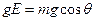 (2分)
(2分)
得: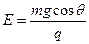 (2分)
(2分)
代入数据:E=1.5×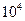 N/C (2分)
N/C (2分)
方向:垂直于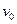 斜向上. (2分)
斜向上. (2分)
(2)由于粒子所受重力、电场力均为恒力,所以粒子的加速度恒定.粒子所受的合外力方向与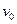 方向相反,所以粒子做匀减速运动. (3分)
方向相反,所以粒子做匀减速运动. (3分)
由:mgsinq =ma解得: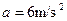 (3分)
(3分)
本题难度:一般
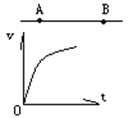
3、选择题 AB是电场中的一条电场线,若将一负电荷从A点处自由释放,负电荷沿电场线从A到B运动过程中的速度图线如图所示,则A.B两点的电势高低和场强的大小关系是( )
A.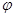 A>
A>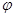 B,EA>EB B.
B,EA>EB B. A>
A> B,EA<EB
B,EA<EB
C. A<
A< B,EA>EB D.
B,EA>EB D. A<
A< B,EA<EB
B,EA<EB
参考答案:C
本题解析:负电荷受力方向与电场方向相反,故电场线方向应该是由B→A,顺着电场线方向,电势依次降低,故 A<
A< B;v-t图象中斜率的大小表示加速度的大小,则aA>aB,而a=
B;v-t图象中斜率的大小表示加速度的大小,则aA>aB,而a=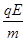 ,故EA>EB。选项C正确。
,故EA>EB。选项C正确。
考点:本题旨在考查静电场。
本题难度:一般
4、选择题 下列粒子从初速度为零的状态经过电压为U的电场加速后,速度最大的是
A.质子
B.氘核
C.α粒子(氦核)
D.钠离子
参考答案:A
本题解析:根据动能定理可得 可得质子获得的速度最大。A正确。
可得质子获得的速度最大。A正确。
本题难度:简单
5、计算题 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线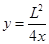 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
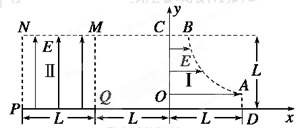
(1)求从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度;
(2) 求(1)中的电子离开MNPQ时的坐标;
(3)证明在电场区域Ⅰ的AB曲线上任何一点处,由静止释放电子恰能从MNPQ区域左下角P点离开;
参考答案:(1) v=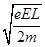 ;(2)(-2L,0);
;(2)(-2L,0);
(3)离开点的横坐标X1=-2L,纵坐标y1=y-y’=0,即(-2L,0)为P点。
本题解析:
试题分析: (1)? B点坐标( , L),在电场I中电子被加速到v,由动能定理
, L),在电场I中电子被加速到v,由动能定理
eE =
= ,解得v=
,解得v=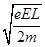
(2)电子进入电场II做类平抛运动,有
t=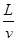 ?;
?;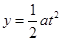 ;
;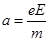
所以横坐标x=" -" 2L;纵坐标y=L-y=0即为(-2L,0)
(3)设释放点在电场区域I的AB曲线边界,其坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,有eEx= ;t=
;t=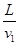 ;
;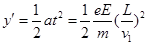 ?;
?;
所以离开点的横坐标X1=-2L,纵坐标y1=y-y’=0,即(-2L,0)为P点。
本题难度:困难