1、简答题  甲、乙两颗人造地球卫星，其线速度大小之比为以2：1，
求：
（1）这两颗卫星的转动半径之比；
（2）转动角速度之比；
（3）转动周期之比；
（4）向心加速度大小之比．

参考答案：由题意知v1v2=21
（1）对于卫星万有引力提供圆周运动的向心力得：
GmMR2=mv2R可得对于不同卫星运动半径与线速度的平方成反比即：R=GMv2
∴R1R2=v22v12=(12)2=14
（2）线速度与角速度的关系为v=Rω，所以有：ω1ω2=v1R1v2R2=v1v2×R2R1=21×41=81；
（3）据T=2πω得：T1T2=ω2ω1=18；
（4）圆周运动向心加速度a=Rω2得a1a2=R1R2×ω12ω22=14×(81)2=161
答：这两颗卫星的转动半径之比1：4；
（2）转动角速度之比8：1；
（3）转动周期之比1：8；
（4）向心加速度大小之比16：1．

本题解析：

本题难度：一般

2、选择题  已知地球同步卫星离地面的高度约为地球半径的6倍，若某行星的平均密度为地球平均密度的一半，它的同步卫星距其表面的高度是其半径的2.5倍，则该行星的自转周期约为
[? ]
A．6小时
B．12小时
C．24小时
D．36小时

参考答案：B

本题解析：

本题难度：一般

3、选择题  2008年9月25日我国利用、刘伯明、景海鹏成功送入太空，神舟七号飞船成功变轨，由原来的椭圆轨道变为距地面高度为h的圆形轨道．已知飞船的质量为m，地球半径为R，地面处的重力加速度为g，引力常量为G，由以上数据可推知
[? ]
A.飞船在上述圆轨道上运行时宇航员由于不受引力作用而处于失重状态
B.飞船在上述圆轨道上运行的周期等于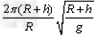
C.飞船在上述圆轨道上运行的动能等于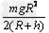
D.地球的平均密度为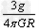

参考答案：BCD

本题解析：

本题难度：一般

4、填空题  人类发射的空间探测器进入某行星的引力范围后，绕该行星做匀速圆周运动．已知该行星的半径为R，探测器运行轨道在其表面上空高h处，运行周期为T．求该行星的质量M=______，它的平均密度ρ=______．

参考答案：空间探测器绕该行星 做匀速圆周运动，行星的万有引力提供向心力，由万有引力定律和牛顿第二定律得：
? GMm(R+h)2=4π2m(R+h)T2
? 解得求该行星的质量M=4π2(R+h)3GT2
行星的体积V=43πR3，又∵ρ=MV
联立以上三式解得行星的平均密度ρ=3π(R+h)3GT2?R3

故答案为：该行星的质量M=4π2(R+h)?3GT2，它的平均密度ρ=3π(R+h)3GT2R3．

本题解析：

本题难度：一般

5、选择题  同一遥感卫星离地面越近时，获取图象的分辨率也就越高．则当图象的分辨率越高时，卫星的
[? ]
A．向心加速度越小?
B．角速度越小?
C．线速度越小?
D．周期越小

参考答案：D

本题解析：

本题难度：简单