1、计算题 1930年,科学家发现:在真空条件下用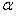 粒子轰击
粒子轰击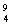 Be时,会产生一种贯穿能力强且不带电、质量与质子很接近的粒子和另一种原子核。
Be时,会产生一种贯穿能力强且不带电、质量与质子很接近的粒子和另一种原子核。
(1)写出这个过程的核反应方程;
(2)若该种粒子以初速度v0与一个静止的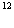 C核发生碰撞,但没有发生核反应,该粒子碰后的速率为v1,运动方向与原运动方向相反。求
C核发生碰撞,但没有发生核反应,该粒子碰后的速率为v1,运动方向与原运动方向相反。求 C核与该粒子碰撞后的速率。
C核与该粒子碰撞后的速率。
参考答案:解:(1)核反应方程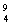 Be+
Be+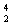 He →
He →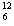 C+
C+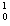 n
n
(2)由动量守恒定律得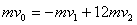
解得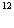 C核碰撞后的速率
C核碰撞后的速率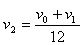
本题解析:
本题难度:一般
2、计算题 如图所示,一辆质量是m=2kg的平板车左端放有质量M=3kg的小滑块,滑块与平板车之间的动摩擦因数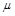 =0.4,开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求:
=0.4,开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求:
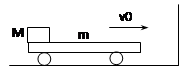
(1)平板车每一次与墙壁碰撞后向左运动的最大距离.
(2)平板车第二次与墙壁碰撞前瞬间的速度v.
(3)为使滑块始终不会滑到平板车右端,平板车至少多长?
参考答案:(1)0.33m(2) (3)0.833m
(3)0.833m
本题解析:(1)设第一次碰墙壁后,平板车向左移动s,速度为0.由于体系总动量向右,平板车速度为零时,滑块还在向右滑行.
动能定理 ?①
?①
 ?②
?②
代入数据得 ?③
?③
(3)假如平板车在第二次碰撞前还未和滑块相对静止,那么其速度的大小肯定还是2m/s,滑块的速度则大于2m/s,方向均向右.这样就违反动量守恒.所以平板车在第二次碰撞前肯定已和滑块具有共同速度v.此即平板车碰墙前瞬间的速度.
 ?④
?④
∴ ?⑤
?⑤
代入数据得 ?⑥
?⑥
(3)平板车与墙壁发生多次碰撞,最后停在墙边.设滑块相对平板车总位移为l,则有 ?⑦
?⑦
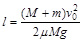 ?⑧
?⑧
代入数据得 ?⑨
?⑨
l即为平板车的最短长度.
本题难度:简单
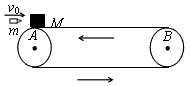
3、计算题 如图所示,质量M=1.0kg的木块随传送带一起以v=2.0m/s的速度向左匀速运动,木块与传送带间的动摩擦因数μ=0.50。当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=3.0×102m/s水平向右的速度击穿木块,穿出时子弹速度v1=50m/s。设传送带的速度恒定,子弹击穿木块的时间极短,且不计木块质量变化,g=10m/s2。求:
(1)在被子弹击穿后,木块向右运动距A点的最大距离;
(2)子弹击穿木块过程中产生的内能;
(3)从子弹击穿木块到最终木块相对传送带静止的过程中,木块与传送带间由于摩擦产生的内能。
参考答案:解:(1)设木块被子弹击穿时的速度为u,子弹击穿木块过程动量守恒
mv0-Mv=mv1+Mu,解得u=3.0m/s
设子弹穿出木块后,木块向右做匀减速运动的加速度为a,根据牛顿第二定律
μmg=ma,解得a=5.0m/s2
木块向右运动到离A点最远时,速度为零,设木块向右移动最大距离为s1
u2=2as1,解得s1=0.90m
(2)根据能量守恒定律可知子弹射穿木块过程中产生的内能为
E=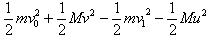
解得E=872.5J
(3)设木块向右运动至速度减为零所用时间为t1,然后再向左做加速运动,经时间t2与传送带达到相对静止,木块向左移动的距离为s2。根据运动学公式
v2=2as2,解得s2=0.40m
t1=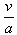 =0.60s,t2=
=0.60s,t2=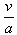 =0.40s
=0.40s
木块向右减速运动的过程中相对传送带的位移为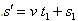 =2.1m
=2.1m
产生的内能Q1=μMg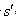 =10.5J
=10.5J
木块向左加速运动的过程中相对传送带的位移为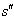 =vt2-s2=0.40m
=vt2-s2=0.40m
产生的内能Q2=μMg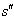 =2.0J
=2.0J
所以整个过程中木块与传送带摩擦产生的内能Q=Q1+Q2=12.5J
本题解析:
本题难度:困难
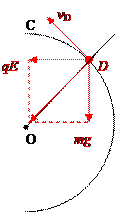
4、简答题 如图所示,在水平向左的匀强电场中,有一光滑绝缘的导轨,导轨由水平部分AB和与它连接的的位于竖直平面的半圆轨道BC构成,AB长为L,圆轨道半径为R.A点有一质量为m电量为+q的小球,以初速度v0水平向右运动而能进入圆轨道.若小球所受电场力与其重力大小相等,重力加速度为g,求:
⑴小球运动到B点时的速度vB
⑵小球能过C点而不脱离圆轨道,v0必须满足的条件.
参考答案:⑴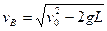 ?⑵
?⑵
本题解析:⑴如图,球从A到B的过程中,由动能定理
 (3分)
(3分)
而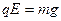 (3分)?故
(3分)?故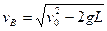 (3分)
(3分)
⑵受力分析知,D点重力和电场力的合力沿半径,轨道弹力N=0时小球速度最小,小球若能过D点则必过C点,则在D点
 (2分)?
(2分)?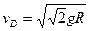 (2分)
(2分)
从B到D的过程中,由动能定理
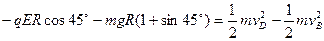 (2分)
(2分)
故 (2分)
(2分)
即小球能过C点而不脱离圆轨道,v0必须满足的条件
 (2分)
(2分)
本题难度:一般
5、简答题 已知氘核质量为2.0136u,中子质量为1.0087u,
He核的质量为3.0150u,(1u相当于931.5MeV的能量)
(1)写出两个氘核聚变成He的核反应方程.
(2)计算上述核反应中释放的核能.
(3)若两个氘核以相等的大小为0.35MeV的动能做对心碰撞即可发生上述核反应,且释放的核能全部转化为机械能,则反应中生成的He核的动能是多少?
参考答案:(1)由质量数守恒和核电荷数守恒,写出核反应方程为:?21H+?21H→?32He+?10n
(2)反应过程中质量减少了:
△m=2×2.0136u-1.0087u-3.0150u=0.0035u
反应过程中释放的核能△E=0.0035×931.5MeV=3.26MeV
(3)设?10n核和?32He的动量分别为P1和P2,由动量守恒定律得:O=P1+P2
由此得P1和P2大小相等
由动能和动量关系E=P22m及?32He核和?10n质量关系
得:中子的动能E1是?32He核动能E2的3倍 即E1:E2=3:1
由能量守恒定律得:E1+E2=△E+2×0.35
由以上可以算出:E2=0.99MeV
答:(1)核反应方程为:?21H+?21H→?32He+?10n.
(2)上述核反应中释放的核能为3.26MeV.
(3)反应中生成的?32He核的动能是0.99MeV.
本题解析:
本题难度:一般