1、选择题 在半径为R的圆形区域内有垂直于纸面向内的匀强磁场,磁感应强度为B,一质量为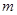 、电荷量为
、电荷量为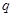 的负电荷,以速率
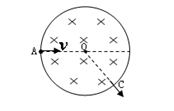
的负电荷,以速率 从A点垂直于磁场方向正对着磁场的圆心射入后从C点射出,已知角AOC为1200,则该粒子在磁场中的运动时间为:(?)
从A点垂直于磁场方向正对着磁场的圆心射入后从C点射出,已知角AOC为1200,则该粒子在磁场中的运动时间为:(?)
A.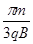
B.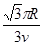
C.
D.
参考答案:AB
本题解析:分析:带电粒子在磁场中由洛伦兹力提供向心力,使粒子做匀速圆周运动.从而可推导出轨道半径公式与周期公式,由题中运动的时间与磁感应强度可求出粒子的比荷,由于圆磁场的半径未知,所以无法求出轨道半径,也不能算出粒子的初速度.
解答:解:带电粒子在洛伦兹力作用下做匀速圆周运动,则有:Bqv=m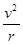
由几何关系可得:R=rtan30°
再由周期公式可得:T=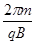 ,而运动时间为:t=
,而运动时间为:t=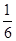 T=
T=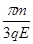
或者t=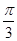 ×
×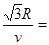
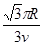
故选:AB.
点评:带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径,同时还利用圆弧的几何关系来帮助解题.值得注意是圆形磁场的半径与运动轨道的圆弧半径要区别开来.
本题难度:简单
2、选择题 一个运动电荷在某个空间里没有受到洛伦兹力的作用,那么
[? ]
A.这个空间一定没有磁场
B.这个空间不一定没有磁场
C.这个空间可能有方向与运动方向平行的磁场
D.这个空间可能有方向与运动方向垂直的磁场
参考答案:BC
本题解析:
本题难度:简单
3、选择题 如图所示,两个横截面分别为圆形和正方形的区域内有磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入。则下面判断错误的是
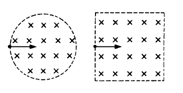
A.两电子在两磁场中运动时,其半径一定相同
B.两电子在磁场中运动的时间有可能相同
C.进入圆形磁场区域的电子可能先飞离磁场
D.进入圆形磁场区域的电子可能后飞离磁场
参考答案:D
本题解析:带电粒子在磁场中的运动专题.
分析:电子在磁场中做匀速圆周运动,洛伦兹力提供向心力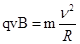 ,整理出半径表达式判断半径是否相同;运动时间的判断可以根据转过的圆心角的大小;比较哪个磁场电子先出磁场,可以做出多个轨迹比较.
,整理出半径表达式判断半径是否相同;运动时间的判断可以根据转过的圆心角的大小;比较哪个磁场电子先出磁场,可以做出多个轨迹比较.
解:电子在磁场中做匀速圆周运动,洛伦兹力提供向心力: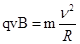 ,整理得
,整理得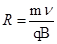 ,两过程电子速度v相同,所以半径相同.粒子在磁场中的可能运动情况如图所示,
,两过程电子速度v相同,所以半径相同.粒子在磁场中的可能运动情况如图所示,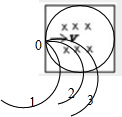
电子从O点水平进入由于它们进入圆形磁场和矩形磁场的轨道半径、速度是相同的,我们把圆形磁场和矩形磁场的边界放到同一位置如图所示,由图可以看出进入磁场区域的电子的轨迹1,先出圆形磁场,再出矩形磁场;进入磁场区域的电子的轨迹2,同时从圆形与矩形边界处磁场;进入磁场区域的电子的轨迹3,先出圆形磁场,再出矩形磁场;所以电子不会先出矩形的磁场,即进入圆形区域的电子一定不会后飞离磁场,
本题难度:简单
4、选择题 下列说法正确的是( )
A.洛伦兹力对带电粒子永远不做功
B.运动电荷在某处不受洛伦兹力作用,则该处的磁感应强度一定为零
C.运动电荷在磁感应强度不为零的地方,一定受到洛伦兹力作用
D.洛伦兹力既不能改变带电粒子的动能,也不能改变带电粒子的速度
参考答案:A、洛伦兹力的方向与速度方向垂直,所以洛伦兹力对带电粒子不做功.故A正确.
? B、将粒子运动的方向v∥B,不受洛伦兹力,但磁感应强度不为0.故B错误,C错误.
? D、洛伦兹力只改变速度的方向,不改变速度的大小.故D错误.
故选A.
本题解析:
本题难度:简单
5、选择题 赤道附近地磁场方向向北,同时存在方向竖直向下的电场.若在该处发射一电子,电子沿直线飞行而不发生偏转.则该电子的飞行方向为( )
A.水平向东
B.水平向西
C.竖直向上
D.竖直向下
参考答案:既有电场也有磁场,电子沿直线飞行而不发生偏转,说明电子受力平衡,电场力的方向是竖直向上的,所以洛伦兹力的方向就是竖直向下的,根据左手定则可以知道电子的飞行方向为水平向东,所以A正确,BCD错误.
故选A.
本题解析:
本题难度:简单
Let those who know the way go before. 让识途的人先行。