1、计算题  分已知“嫦娥一号”绕月飞行轨道近似为圆形，距月球表面高度为H，飞行周期为T，
月球的半径为R，引力常量为G。求：
（1）“嫦娥一号”绕月飞行时的线速度大小；
（2）月球的质量；
（3）若发射一颗绕月球表面做匀速圆周运动的近月飞船，则其绕月运行的线速度应为多大．

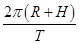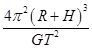参考答案：（1）　　（2）　　（3）

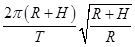
本题解析：（1）“嫦娥一号”的轨道半径r=R+H，根据线速度与轨道半径和周期的关系得：
“嫦娥一号”运行的线速度
（2）设月球质量为M，“嫦娥一号”的质量为m，根据万有引力定律和牛顿第二定律，
对“嫦娥一号”绕月飞行有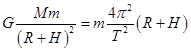　
解得：
（3）设绕月球表面做匀速圆周运动的飞船的质量为m0，线速度为v0，绕月球表面做匀速圆周运动的飞船轨道半径约R．根据万有引力定律和牛顿第二定律，对飞船绕月飞行有?
又，联立可解得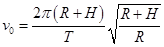

本题难度：简单

2、简答题  如图所示，两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ=37°的绝缘斜面上，两导轨间距L=1m，导轨的电阻可忽略．M、P两点间接有阻值为R?的电阻．一根质量m=1kg、电阻r=0.2Ω的均匀直金属杆ab放在两导轨上，与导轨垂直且接触良好．整套装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向垂直斜面向下．自图示位置起，杆ab受到大小为F=0.5v+2（式中v为杆ab运动的速度，力F的单位为N）、方向平行导轨沿斜面向下的拉力作用，由静止开始运动，测得通过电阻R的电流随时间均匀增大．g取10m/s2，sin37°=0.6．
（1）试判断金属杆ab在匀强磁场中做何种运动，并请写出推理过程；
（2）求电阻的阻值R；
（3）求金属杆ab自静止开始下滑通过位移x=1m所需的时间t和该过程中整个回路产生的焦耳热Q．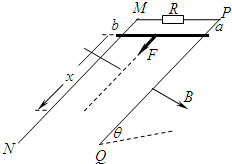

参考答案：（1）金属杆做匀加速运动（或金属杆做初速为零的匀加速运动）．
通过R的电流I=ER+r=BLvR+r，因通过R的电流I随时间均匀增大，即杆的速度v随时间均匀增大，杆的加速度为恒量，故金属杆做匀加速运动．
（2）对杆，根据牛顿第二定律有：F+mgsinθ-BIL=ma
将F=0.5v+2代入得：
? 2+mgsinθ+（0.5-B2L2R+r）v=ma，
因a与v无关，所以
? a=2+mgsinθm=8m/s2
代入得0.5-B2L2R+r=0?得
? R=0.3Ω
（3）由x=12at2得，所需时间t=

本题解析：

本题难度：一般

3、计算题  如图，一劲度k=800N/m的轻弹簧两端各焊接着质量均为m=12kg的物体A、B，竖直静止在水平地面上。现要加_竖直向上的力F在上面物体A上，使A开始向上做匀加速运动，经0.4s，B刚要离开地面，整个过程弹簧都处于弹性限度内（g=10m/s）。求此过程所加外力F的最大值和最小值。

参考答案：，

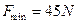
本题解析：初始A未上升时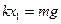，?（1分）
末态B将要离地时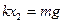?（1分）
A的位移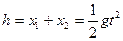?（1分）
初始时F最小?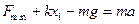?（2分）
末态时F最大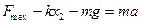?（2分）
解得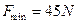?（1分）
?（1分）

本题难度：简单

4、计算题  （11分）汽车在水平直线公路上行驶，额定功率为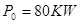，汽车行驶过程中所受阻力恒为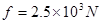，汽车的质量。若汽车从静止开始做匀加速直线运动，加速度的大小为，汽车达到额定功率后，保持额定功率不变继续行驶求：（1）汽车在整个运动过程中所能达到的最大速度；
（2）匀加速运动能保持多长时间；
（3）当汽车的速度为20m/s时的加速度

参考答案：（1）32m/（2）12.8s（3）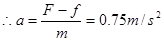

本题解析：（1）汽车匀速行驶时F=f，达到最大速度Vm，
则Vm=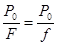=32m/s----2分，
（2）根据F-f="m" a得F=f＋m a=5×103N---2分
V=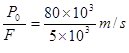="16" m/s-----2分
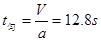--1分
（3）v=20m/s>16m/s?故车变加速阶段，保持P0不变
则F=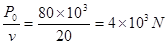--1分
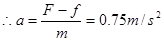--2分
点评：难度较小，熟记机车启动的两种形式和各物理量的变化

本题难度：一般

5、计算题  如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°（sin37?=0.6；cos37?=0.8）的固定且足够长的粗糙斜面上，对物体施以平行于斜面向上的拉力F，t1＝1s时撤去拉力，物体运动的部分v—t图像如图乙所示(物体与斜面间的最大静摩擦力等于滑动摩擦力，g取10 m/s2)试求：

（1）拉力F的大小。
（2）t＝4s时物体的速度v的大小。

参考答案：(1) F=30N (2) 2m/s

本题解析：（1）设力F作用时物体的加速度为a1，对物体进行受力分析，
y轴? N —mgcosθ=" 0" ?1分
公式? f =" μ" N ?1分
x轴　F－mgsinθ－μmgcosθ＝ma1? 3分
撤去力后，由牛顿第二定律有mgsinθ＋μmgcosθ＝ma2? 3分
根据图像可知：a1＝20m/s2，a2＝10m/s2，代入解得F=30N，μ=0．5。? 4分
（2）设撤去力后物体运动到最高点时间为t2，
v1＝a2t2，解得t2＝2s，
则物体沿着斜面下滑的时间为t3=t－t1－t2=1s，
设下滑加速度为a3，由牛顿第二定律mgsinθ－μmgcosθ=ma3，
有a3="2" m/s2，t＝4s时速度v＝a3t3＝2m/s。? 4分
点评：本题首先要理解速度的物理意义：斜率等于加速度，“面积”等于位移．也可以根据动量定理和动能定理结合求解．

本题难度：一般