微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速运动,(sin37°=0.6,cos37°=0.8)求:

小题1:雪橇对地面的压力大小;
小题2:雪橇与水平地面的动摩擦因数的大小.
参考答案:
小题1:340N
小题2:0.24
本题解析:(1)经对小孩和雪橇整体受力分析得:
竖直方向:Fsinθ+FN=mg? 2分
解得 FN= mg—Fsinθ="340N?" 2分
雪橇对的地面压力 是地面对雪橇支持力F N的反作用力,所以雪橇对的地面压力:
是地面对雪橇支持力F N的反作用力,所以雪橇对的地面压力:
 =F N="340N?" 1分
=F N="340N?" 1分
(2)水平方向:Fcosθ—F f="0?" 2分? F f=μF N ?
由上式解得:μ=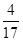 ="0.24?" 2分
="0.24?" 2分
本题难度:简单
2、计算题 (16分)如图所示,一根内壁光滑的直角三角形玻璃管子处于竖直平面内,倾斜角为θ= 37°,让两个小球分别从顶点A由静止开始出发,一个球沿AC滑下,到达C所用的时间为t1,另一个球竖直自由下落经过B到达C,所用的时间为t2,在转弯处有个极小的光滑圆弧,可确保小球转弯时无机械能损失,且转弯时间可以忽略不计。问:
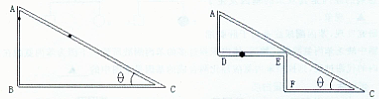
(1)计算t1∶ t2的值;
(2)若用同样的玻璃管把ABC轨道改为如图所示的ADEFC(在转弯处均有个极小的光滑圆弧),仍让小球从A静止开始运动,依次通过D、E、F后到达C点所用时间为t3,试定性说明t3和t1、t2的大小关系。
参考答案:解:(1)设内壁光滑的直角三角形玻璃管三边AB、BC、AC分别为3l、4l、5l,由AC边滑下,根据牛顿第二定律可得加速度a=gsinθ=6m/s2。
由5l=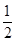 at12,解得t1=5
at12,解得t1=5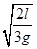 。
。
沿ABC滑下,在AB段由3l=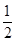 gt212,解得t21=
gt212,解得t21=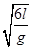 。
。
沿水平段BC运动速度,v= gt21=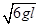 ,
,
由4l=vt22,解得t22=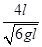 。
。
t2= t21 +t22=5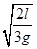 。
。
t1∶ t2=1 ∶ 1。
即两球同时释放同时到达。
(2)若用同样的玻璃管把ABC轨道改为如图所示的ADEFC,若球沿ADEF到C,则可判断小球在水中管中运动时间是相等的。沿DE运动时速度比在BC中运动时要小,故在水平管中运动时间长,所以沿ABC管运动时间比沿ADEFC的时间要短一些,所以t3> t2= t1.
本题解析:应用牛顿第二定律和运动学公式列方程解答。
本题难度:一般
3、计算题 放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示. 取重力加速度g=10m/s2.试利用两图线求:
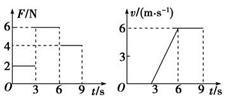
(1)物块在0~9s内发生的位移;
(2)物块在3~6s的加速度大小;
(3)物块与地面间的动摩擦因数.
参考答案:(1)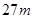 (2)
(2)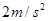 (3)
(3)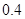
本题解析:(1)由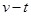 图象可知,
图象可知,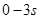 物块处于静止状态,
物块处于静止状态, 物块做匀加速直线运动,
物块做匀加速直线运动,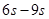 物块做匀速直线运动,因速度时间图线与坐标轴围成的“面积”表示位移,于是得:
物块做匀速直线运动,因速度时间图线与坐标轴围成的“面积”表示位移,于是得:
物块在0~9s内发生的位移为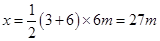
(2)由速度图象的斜率大小等于加速度大小知,物块在3~6s的加速度大小:
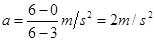
(3)设物块质量为m,与地面间的动摩擦因数为 ?,滑动摩擦力为
?,滑动摩擦力为
由图知,在 内物块做匀速直线运动,受力平衡,于是
内物块做匀速直线运动,受力平衡,于是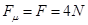
在 内物块做匀加速直线运动,由牛顿第二定律得:
内物块做匀加速直线运动,由牛顿第二定律得:
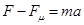 ?
?
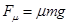 ?
?
将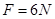 ,
,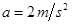 ,
,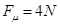 代入以上两式解得:
代入以上两式解得: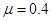
本题难度:一般
4、计算题 (21分) 如图所示,在光滑水平桌面上放有长木板C,在C上左端和距左端x处各放有小物块A和B,A、B的体积大小可忽略不计,A、B与长木板C间的动摩擦因数为μ,A、B、C的质量均为m,开始时,B、C静止,A以某一初速度v0向右做匀减速运动,设物体B与板C之间的最大静摩擦力等于滑动摩擦力.求:?

(1)物体A运动过程中,物块B受到的摩擦力大小.?
(2)要使物块A、B相碰,物块A的初速度v0应满足的条件.
参考答案:(1)fb = 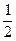 μmg
μmg
(2)v0>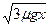
本题解析:
(1)设A在C板上滑动时,B相对于C板不动,则对B、C有?
μmg=2ma?(3分)??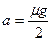 ?
?
B受到的摩擦力fb = ma =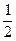 μmg?(2分)
μmg?(2分)
由于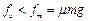 所以fb =
所以fb = 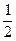 μmg(2分)
μmg(2分)
(2)要使物块A刚好与物块B发生碰撞,物块A运动到物块B处时,A、B的速度相等,设物块A的位移为s1?木板C在此过程中的位移为s2,,
对A :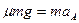 ?(2分)?
?(2分)?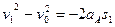 (2分)
(2分)
对BC: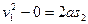 (2分)
(2分)
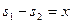 (2分)
(2分)
?v1= v0-μgt =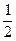 μgt(4分)?得v1= v0/3?
μgt(4分)?得v1= v0/3?
联立上述各式解得v0 =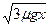 ?(2分)
?(2分)
要使物块A、B发生相碰的条件是v0>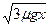
本题难度:简单
5、简答题 质量均为m=0.1kg的两个小物体A和B,静止放在足够长的水平面上,相距L=12.5m.它们跟水平面间的动摩擦因数均为μ=0.2,其中A带电荷量为q=3×10-4C的正电荷,与水平面的接触是绝缘的,B不带电.现在水平面附近空间加一水平向右的匀强电场,场强E=103?N/C,A便开始向右运动,并与B发生多次对心碰撞,碰撞过程时间极短,碰撞过程中无机械能损失,A带电量不变,B始终不带电,重力加速度g取10m/s2.

求:
(1)A与B第1次碰撞后B的速度大小;
(2)A与B从第2次碰撞到第3次碰撞过程中B运动的位移;
(3)整个运动过程中A、B同水平面摩擦产生热量的总和.
参考答案:(1)对A,根据牛顿第二定律 Eq-μmg=maA,
解得加速度 aA=1m/s2
根据公式v2A1=2aAL,解得A与B碰前速度 vA1=5m/s
碰撞交换速度,第1次碰后,A的速度为0,B的速度 vB1=vA1=5m/s.
(2)对B,根据牛顿第二定律 μmg=maB,解得加速度大小aB=2m/s2,
每次碰后B作匀减速运动,因其加速度大于A的加速度,所以B先停,之后A追上再碰,每次碰后A的速度均为0,然后加速再与B发生下次碰撞.
第1次碰撞:xB1为第1次碰后B的位移,则? v2B1=v2A1=2aBxB1,
解得,碰后B运动的位移为xB1=6.25m
第2次碰撞:碰撞前A的速度为vA2,则v2A2=2aAxB1,
由上两式得
? v2A2v2A1=aAaB=12
得:xA2L=xB1L=v2A2v2A1=aAaB=12
以此类推,第2次碰撞后B运动的位移
xB2=(aAaB)2L=3.125m.
(3)根据第(2)问的分析,经过n次碰撞后B的速度 vBn=vA1(
本题解析:
本题难度:一般