1、填空题  一高度为h的光滑弧形轨道固定在水平面上，如图所示．质量为m的物体A从轨道顶端由静止开始下滑到底面时速度的大小为______，此过程中重力对物体A做功为______．（空气阻力不计）

参考答案：根据动能定理得，mgh=12mv2-0，解得v=

本题解析：

本题难度：简单

2、计算题  如图所示，两个四分之一圆弧形的光滑轨道AB、CD和粗糙水平轨道BC之间光滑连接。AB弧的半径为R，CD弧的半径为0.7R。BC间距离为3R。质量为m的滑块P（可视为质点）从AB弧的上端从静止释放，第一次通过C点后恰好能到达CD弧的最高点D。重力加速度为g。求：

小题1:滑块与水平轨道BC间的动摩擦因数；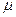
小题2:从释放到停止运动滑块在水平轨道BC上滑动的总路程s；
小题3:滑块P第一次到达两圆弧最下端的B点和C点时对圆弧轨道的压力大小之比NB：NC。

参考答案：
小题1: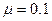
小题2:s=10R
小题3: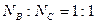

本题解析：（1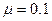）（提示：从A到D全过程对滑块用动能定理，mg（R-0.7R）=）
（2）s="10R?" （提示：从A点释放到最终停止运动全过程对滑块用动能定理，。）
（3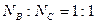）?（提示：两端圆弧半径不同，但都有，而对应的压力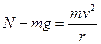，得N =3mg，与半径大小无关。）

本题难度：一般

3、计算题  一轻弹簧的左端固定在墙壁上，右端自由，一质量为m的滑块从距弹簧右端L0的P点以初速度v0正对弹簧运动，如下图所示，滑块与水平面的动摩擦因数为μ，在与弹簧碰后反弹回来，最终停在距P点为L1的Q点，求：在滑块与弹簧碰撞过程中弹簧最大压缩量为多少？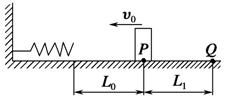

参考答案：－－L0

本题解析：设弹簧最大压缩量为x，在滑块向左运动的过程中，由动能定理可得：
－μmg(x＋L0)－W弹＝0－mv20? ①
在滑块返回的过程中，由动能定理得：
W弹－μmg(x＋L0＋L1)＝0? ②
由①②得：x＝－－L0

本题难度：一般

4、计算题  如图所示，光滑半圆形轨道处于竖直平面内，半圆轨道与光滑的水平地面相切于半圆的端点A。一质量为m的小球在水平地面上的C点受水平向左的恒力F由静止开始运动，当运动到A点时撤去恒力F，小球沿竖直半圆轨道运动到轨道最高点B点，最后又落在水平地面上的D点（图中未画出）。已知A、C间的距离为L,重力加速度为g。

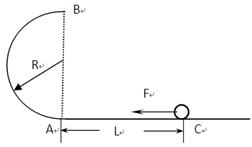
（1）若轨道半径为R，求小球到达圆轨道B点时对轨道的压力FN;
（2）为使小球能运动到轨道最高点B，求轨道半径的最大值Rm；
（3）轨道半径R多大时，小球在水平地面上的落点D到A点的距离最大？最大距离xm是多少？

参考答案：（1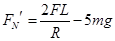），方向竖直向上?（2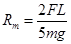）?（3）?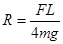

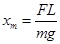
本题解析：（1）设小球到达B点时速度为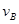，根据动能定理有

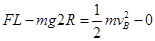
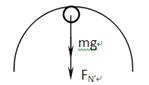
设B点时轨道对小球的压力为，对小球在B点时进行受力分析如图，则有


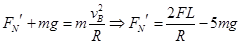
根据牛顿第三定律可知小球对轨道的压力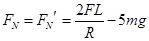，方向竖直向上
（2）小球能够到达最高点的条件是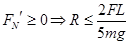
故轨道半径的最大值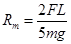
（3）从B点飞出后做平抛运动，落地时间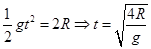
D到A的距离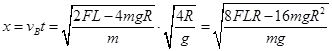
相当于二次函数求最大值的问题，最大值在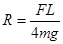时取到
（因为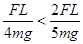，所以最大值可以取得到）
代入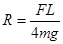，得到此时最大距离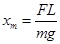
点评：小球在最高点时合外力等于向心力，过最高点的临界条件是小球对轨道的压力为零，即重力等于向心力。

本题难度：一般

5、简答题  如图所示，竖直放置的半圆形绝缘轨道半径为R，下端与光滑绝缘水平面平滑连接，整个装置处于方向竖直向上的匀强电场E中．一质量为m、带电荷量为+q的物块（可视为质点），从水平面上的A点以初速度v0水平向左运动，沿半圆形轨道恰好通过最高点C，场强大小为E（E小于

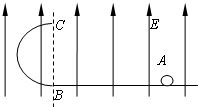
参考答案：

本题解析：

本题难度：一般