1、选择题  如图所示，在光滑水平面上，有一个粗细均匀的单匝正方形闭合线框abcd．t=0时刻，线框在水平外力的作用下，从静止开始向右做匀加速直线运动，bc边刚进入磁场的时刻为t1，ad边刚进入磁场的时刻为t2，设线框中产生的感应电流的大小为i，ad边两端电压大小为U，水平拉力大小为F，则下列i、U、F随运动时间t变化关系图像正确的是

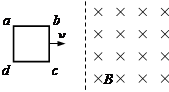
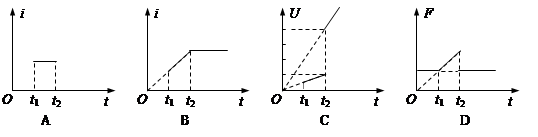
参考答案：C

本题解析：由于线框进入磁场是做匀加速直线运动，故速度不逐渐增加的，所以进入磁场时产生的电动势也是逐渐增加的，由于线框的电阻不变，故线框中的电流也是逐渐增加的，选项A错误；当线框全部进行磁场后，由于穿过线框的磁通量不变，故线框中的电动势为0，所以线框里的电流也为0，所以选项B错误；由于线框在进入磁场的过程中的电流是均匀增加的，故ad边两端电压也是均匀增加的，但当线框全部进入磁场后，ad间的电压相当于一个导体棒在磁场中切割磁感线而产生的感应电压，该电压随运动速度的增大而增大，且大于t2时刻时ad间的电压，故选项C正确；而对线框的拉力，在线框进入磁场前，由于线框做加速运动，故需要一定的拉力，进入磁场后，线框中的感应电流是均匀增加的，会产生阻碍线框运动的也是均匀增大的安培力，故需要的拉力也是均匀增大的，即F=ma+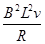，可见拉力F与速度v(或时间t)成线性关系，不是正比关系，其图像不过原点，所以选项D错误。
考点：电磁感应，安培力大小的判断。

本题难度：一般

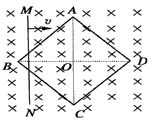
2、简答题  t=0时，磁场在xOy平面内的分布如图所示，其磁感应强度的大小均为B0，方向垂直于xOy平面，相邻磁场区域的磁场方向相反，每个同向磁场区域的宽度均为L0，整个磁场以速度v沿x轴正方向匀速运动．若在磁场所在区间内放置一由n匝线圈组成的矩形线框abcd，线框的bc边平行于x轴．bc=LB、ab=L，LB略大于L0，总电阻为R，线框始终保持静止．求：
（1）线框中产生的总电动势大小和导线中的电流大小；
（2）线框所受安培力的大小和方向．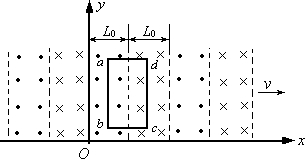

参考答案：（1）线框相对于磁场向左做切割磁感线的匀速运动，切割磁感线的速度大小为v，任意时刻线框中产生的总电动势大小为
? E=2nB0Lv
导线中电流的大小为 I=ER=2nB0LvR
（2）线框所受安培力的大小 F=2nB0LI=4n2B20L2vR
由左手定则判断知，线框所受的安培力方向始终沿x轴正方向．
答：
（1）线框中产生的总电动势大小是2nB0Lv，导线中的电流大小是2nB0LvR；
（2）线框所受安培力的大小为4n2B20L2vR，方向始终沿x轴正方向．

本题解析：

本题难度：一般

3、计算题  如图所示，边长L＝0.20m的正方形导线框ABCD由粗细均匀的同种材料制成，正方形导线框每边的电阻R0＝1.0Ω，金属棒MN与正方形导线框的对角线长度恰好相等，金属棒MN的电阻r＝0.20Ω。导线框放置在匀强磁场中，磁场的磁感应强度B＝0.50T，方向垂直导线框所在平面向里。金属棒MN与导线框接触良好，且与导线框对角线BD垂直放置在导线框上，金属棒上的中点始终在BD连线上。若金属棒以v＝4.0m/s的速度向右匀速运动，当金属棒运动至AC位置时，求：
（1）金属棒产生的电动势大小；
（2）金属棒MN上通过的电流大小和方向；
（3）导线框消耗的电功率。

参考答案：解：（1）金属棒产生的电动势大小为：E＝BLv＝0.4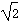V≈0.57V
（2）金属棒运动到AC位置时，导线框左、右两侧电阻并联，其并联电阻大小为R并＝1.0Ω
根据闭合电路欧姆定律I＝≈0.48A
根据右手定则判定，电流方向从N到M
（3）导线框的功率为：P框＝I2R并≈0.23W

本题解析：

本题难度：一般

4、简答题  如图所示，一个U形导体框架，其宽度L=1m，框架所在平面与水平面的夹用α=30°．其电阻可忽略不计．设匀强磁场与U形框架的平面垂直．匀强磁场的磁感强度B=0.2T．今有一条形导体ab，其质量为m=0.5kg，有效电阻R=0.1Ω，跨接在U形框架上，并且能无摩擦地滑动，求：在棒达到最大速度vm时，电阻R上的电功率．（g=10m/s2）．

参考答案：导体棒切割磁感线产生的感应电动势：E=BLv，
电流：I=ER=BLvR，
棒受到的安培力：FB=BIL=B2L2vR，
当棒做匀速直线运动时，速度最大，由平衡条件得：
B2L2vmR=mgsinα，
克服安培力做功转化为电能，电阻消耗的电功率等于克服安培力做功功率：
P=FBv=mgsinα×mgRsinαB2L2=（mgsinα）2RB2L2=（0.5×10×sin30°）2×0.10．22×12=15.625W；
答：电阻R上的功率为15.625W．

本题解析：

本题难度：一般

5、简答题  如图（甲）所示，光滑的平行水平金属导轨MN、PQ相距l，在M点和P点间连接一个阻值为R的电阻，一质量为m、电阻为r、长度也刚好为l的导体棒垂直搁在导轨上a、b两点间，在a点右侧导轨间加一有界匀强磁场，磁场方向垂直于导轨平面，宽度为d0，磁感应强度为B，设磁场左边界到ab距离为d．现用一个水平向右的力F拉导体棒，使它从a、b处静止开始运动，棒离开磁场前已做匀速直线运动，与导轨始终保持良好接触，导轨电阻不计，水平力F-x的变化情况如图（乙）所示，F0已知．求：
（1）棒ab离开磁场右边界时的速度；
（2）棒ab通过磁场区域的过程中整个回路所消耗的电能E；
（3）d满足什么条件时，棒ab进入磁场后一直做匀速运动；
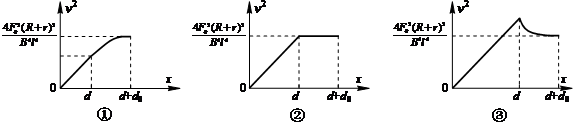
（4）若改变d的数值，定性画出棒ab从静止运动到d+d0的过程中v2-x的可能图线（棒离开磁场前已做匀速直线运动）．

参考答案：
（1）设离开右边界时棒ab速度为v，
则有，感应电动势，E=BLv
闭合电路欧姆定律，I=ER+r?
对棒有?2F0-BIL=0?
解得：v=2F0(R+r)B2L2?
（2）在ab棒运动的整个过程中，根据动能定理：
F0d+2F0d0-W安=12mv2-0?
由功能关系：E电=W安?
解得：E电=F0(d+2d0)-2mF20(R+r)2B4L4?
（3）设棒刚进入磁场时的速度为v0，
则有F0d=12mv20?
当v0=v，即d=2F0m(r+R)2B4L4时，进入磁场后一直匀速运动?
（4）可能的图象如下图所示?




答：（1）棒ab离开磁场右边界时的速度为2F0(R+r)B2L2；
（2）棒ab通过磁场区域的过程中整个回路所消耗的电能为F0(d+2d0)-2mF20(R+r)2B4L4；
（3）当d=2F0m(r+R)2B4L4条件时，棒ab进入磁场后一直做匀速运动；

本题解析：

本题难度：一般