微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 (16分)如图所示,在磁感应强度为B的水平匀强磁场中,有一足够长的绝缘细棒OO′在竖直平面内垂直于磁场方向放置,细棒与水平面夹角为α。一质量为m、带电荷量为+q的圆环A套在OO′棒上,圆环与棒间的动摩擦因数为μ,且μ<tanα,现让圆环A由静止开始下滑,试问圆环在下滑过程中:
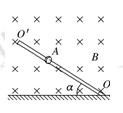
(1)圆环A的最大加速度为多大?获得最大加速度时的速度为多大?
(2)圆环A能够达到的最大速度为多大?
参考答案:(1)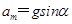 ?
?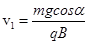 ?(2)
?(2)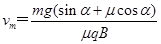
本题解析::(1)由于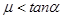 ,即
,即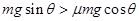 所以环将由静止开始沿棒下滑。环A沿棒运动的速度为
所以环将由静止开始沿棒下滑。环A沿棒运动的速度为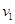 时,受到重力
时,受到重力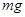 、洛伦兹力
、洛伦兹力 、杆的弹力
、杆的弹力 和摩擦力
和摩擦力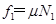 。
。
根据牛顿第二定律,对圆环A受力分析有
沿棒的方向: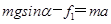 (2分)
(2分)
垂直棒的方向: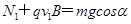 (2分)
(2分)
所以当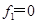 ?(即
?(即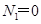 )时
)时
a有最大值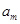 ,且
,且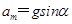
此时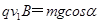 (2分)
(2分)
解得: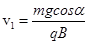 。(2分)
。(2分)
(2)设当环A的速度达到最大值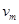 时,环受杆的弹力为
时,环受杆的弹力为 ,摩擦力为
,摩擦力为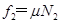 。
。
此时应有 ,即
,即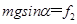 (3分)
(3分)
在垂直杆方向上
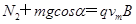 ?(3分)
?(3分)
解得: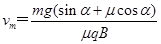 (2分)
(2分)
本题难度:一般
2、选择题 如图所示,一轻质弹簧一端固定在墙上的O点,自由伸长到B点。今用一小物体m把弹簧压缩到A点(m与弹簧不连接),然后释放,小物体能经B点运动到C点而静止。小物体m与水平面间的动摩擦因数μ恒定,则下列说法中正确的是
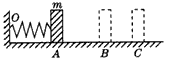
[? ]
A.物体从A到B速度越来越大
B.物体从A到B速度先增大后减小
C.物体从A到B加速度越来越小
D.物体从A到B加速度先减小后增大
参考答案:BD
本题解析:
本题难度:一般
3、简答题 某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔,从左到右,球的编号依次为1、2、3…N,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞…所有碰撞皆为无机械能损失的正碰.(不计空气阻力,忽略绳的伸长,g取10m/s2)
(1)设与n+1号球碰撞前,n号球的速度为vn,求n+1号球碰撞后的速度.
(2)若N=5,在1号球向左拉高h的情况下,要使5号球碰撞后升高16k(16h小于绳长)问k值为多少?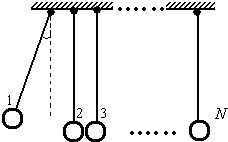
参考答案:(1)本题中的两球相碰,均可看成是“一静一动弹性碰撞模型”.因为每个球的质量依次递减,碰后不会出现入射球反弹的情况.如果入射球质量为m1,被碰球质量为m2,碰前m1的速度为v1,碰后两球的速度分别为v1′、v2′由动量守恒定律和机械能守恒定律得:
m?v1=m1v1′+m2v2′
12mV12=12mV′12+12mV′22
得:V′1=m1-m2m1+m2V1?V′2=2?m1m1+m2V1?
本题主要应用v2′当n取代1时,n+1就取代2.
设n号球质量为m,与n+1号球碰撞后的速度分别为vn′、vn+1′取水平向右为正方向,据题意有n号球与n+1号球碰撞前的速度分别为vn、0、mn+1=kmn?
根据动量守恒,有mnVn=mnV′n+kmnV′n+1…①
根据机械能守恒,有12mnVn2=12mnV′n2+12kmnV′n+12…②
由①②得:V′n+1=2Vnk+1(V′n+1=0舍去)…③
(2)设1号球摆至最低点时的速度为v1,由机械能守恒定律有:
m1gh=12m1V12…④
v1=
本题解析:
本题难度:一般
4、计算题 有一段长为L,与水平面夹角为θ的斜坡路面,一质量为m的木箱放在斜坡底端,质量为4m的人想沿斜坡将木箱推上坡顶,人在地面无滑走动时,人与路面之间的摩擦力是静摩擦力,计算中可认为最大静摩擦力等于滑动摩擦力,重力加速度取g,已知人与路面之间的动摩擦因数为μ,人是沿与斜坡平行的方向用力推木箱的,求:
(1)假设木箱与路面间无摩擦,人推着木箱一起以加速度a向上运动,人受到路面的摩擦力多大?
(2)若木箱与路面间的动摩擦因数也为μ,则人推木箱一起能获得的最大加速度大小是多少?
(3)若木箱与路面间的动摩擦因数也为μ,要将木箱由坡底运送到坡顶,人推木箱一起运动的最短时间是多少?
参考答案:解:(1)把人和木箱作为整体,根据牛顿第二定律
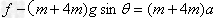 ?
?
得: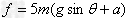
(2)要使木箱能获得的最大加速度,则人与地面间的摩擦力达到最大值。把人和木箱作为整体,根据牛顿第二定律
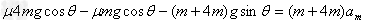
得: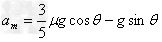
(3)要使木箱由坡底运送到坡顶,人推木箱的时间最短,则人推木箱必须使木箱以最大加速度向上运行,作用一段时间后,人撤去外力,木箱向上做减速运动,到达坡顶速度恰好为零。设人撤去外力时,木箱的速度为v
木箱向上做减速运动的加速度: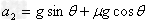 ?
?
对木箱运动全过程有:
人推木箱最短时间为: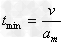 ?
?
联立解得: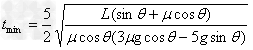
本题解析:
本题难度:一般
5、简答题 一辆质量为5×103kg的汽车,额定功率为60kW,现让汽车保持60kW的功率从水平路面上由静止开始运动,运动中汽车所受阻力恒为车重的0.1倍,(g=10m/s2)求:
(1)启动后0.5s内牵引力做的功;
(2)汽车的加速度为1m/s2时汽车的速度;
(3)汽车的速度为10m/s时的加速度;
(4)汽车行驶过程中能达到的最大速度;
(5)若汽车以2m/s2启动,汽车匀加速运动的时间为多长?
参考答案:(1)由于汽车以额定功率启动,
所以0.5s内牵引力做的功为 W=Pt=60000×0.5J=30000J,
(2)设此时汽车的牵引力为F,由牛顿第二定律得
? F-f=ma,
所以F=ma+f=5000×1+50000×0.1=10000N,
由P=Fv可得
? v=PF=6000010000m/s=6m/s,
(3)设此时汽车的牵引力为F′,
由P=F′v可得
? F′=Pv=6000010N=6000N,
所以加速度为 a=F′-fm=6000-50005000m/s2=0.2m/s2 ,
(4)当牵引力和阻力相等时,汽车达到最大速度,
由 P=FV=fVm 得
? Vm=Pf=600005000m/s=12m/s,
(5)若汽车以2m/s2的加速度匀加速运动,
由牛顿第二定律可得,
? F-f=ma,
所以 F=ma+f=5000×2+5000=15000N,
当功率达到最大时,就是汽车匀加速运动的最后的时刻,
由P=Fv得,
? v=PF=6000015000=4m/s,
所以汽车匀加速运动的时间t=va=42s=2s,
答:(1)启动后0.5s内牵引力做的功是30000J;
(2)汽车的加速度为1m/s2时汽车的速度是6m/s;
(3)汽车的速度为10m/s时的加速度是0.2m/s2 ;
(4)汽车行驶过程中能达到的最大速度是12m/s;
(5)若汽车以2m/s2启动,汽车匀加速运动的时间是2s.
本题解析:
本题难度:一般