微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°。
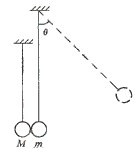
参考答案:解:设小球m的摆线长度为l,小球m在下落过程中与M相碰之前满足机械能守恒:
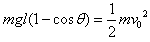 ①
①
m和M碰撞过程满足: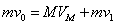 ②
②
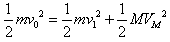 ③
③
联立②③得: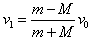 ④
④
说明小球被反弹,而后小球又以反弹速度和小球M发生碰撞,满足:
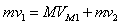 ?⑤
?⑤
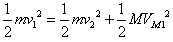 ?⑥
?⑥
解得: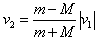 ⑦
⑦
整理得: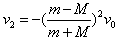 ⑧
⑧
所以: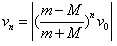 ⑨
⑨
而偏离方向为45°的临界速度满足: ⑩
⑩
联立①⑨⑩代入数据解得,当n=2时,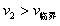
当n=3时,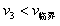
所以最多碰撞3次
本题解析:
本题难度:困难
2、计算题 如图,A、B、C三个木块的质量均为m,置于光滑的水平面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连。将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体。现A以初速v0沿B、C的连线方向朝B运动,与B相碰并粘合在一起。 以后细线突然断开,弹簧伸展,从而使C与A、B分离。已知C离开弹簧后的速度恰为v0。求弹簧释放的势能。

参考答案:解:设碰后A、B和C的共同速度的大小为v,由动量守恒得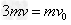 ? ①
? ①
设C离开弹簧时,A、B的速度大小为v1,由动量守恒得 ? ②
? ②
设弹簧的弹性势能为EP,从细线断开到C与弹簧分开的过程中机械能守恒,有
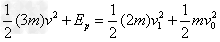 ?③
?③
由①②③式得弹簧所释放的势能为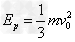
本题解析:
本题难度:一般
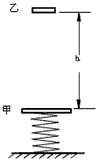
3、计算题 质量m=1.0 kg的甲物体与竖直放置的轻弹簧的上端连接,弹簧下端固定在地面上,如图所示。质量m=1.0 kg的乙物体从甲物体正上方,距离甲物体h=0.40 m处自由落下,撞在甲物体上在极短的时间内与甲物体粘在一起(不再分离)向下运动,它们到达最低点后又向上运动,上升的最高点比甲物体初始位置高H=0.10 m。已知弹簧的劲度系数k=200 N/m,且弹簧始终在弹性限度内,空气阻力可忽略不计,重力加速度g取10 m/s2。求:
(1)乙物体和甲物体碰撞过程中损失的动能;
(2)乙物体和甲物体碰撞后一起向下运动的最大距离。
参考答案:解:(1)设乙物体和甲物体碰撞前瞬间乙物体的速度大小为v1
根据v12=2gh,解得v1=2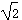 m/s=2.8 m/s
m/s=2.8 m/s
设乙物体和甲物体碰撞后的共同速度大小为v2
由动量守恒定律有mv1=2mv2,解得v2=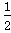 v1=
v1=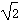 m/s=1.4 m/s
m/s=1.4 m/s
所以碰撞后系统的动能Ek2= (2m)v22=2 J
(2m)v22=2 J
因为甲、乙物体构成的系统碰撞前的动能Ek1=4 J,所以乙物体和甲物体碰撞过程中损失的机械能
ΔE=Ek1-Ek2=2 J
(2)设甲物体静止时弹簧压缩量为x1,根据平衡条件
解得x1=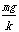 =5.0 cm
=5.0 cm
甲和乙碰撞后做简谐运动,在通过平衡位置时两物体所受合力为零,速度最大,设此时弹簧压缩量为x2
解得x2=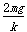 =10 cm
=10 cm
甲物体和乙物体一同上升到最高点,两物体与简谐运动平衡位置的距离,即简谐运动的振幅
A=x2+(H-x1)=15 cm
根据简谐运动的对称性可知,两物体向下运动的最大距离
x=A+(x2-x1)=20 cm
本题解析:
本题难度:困难
4、计算题 【选修3-5选做题】
在光滑的水平面上,甲、乙两物质的质量分别为m1、m2,它们分别沿东西方向的一直线相向运动,其中甲物体以速度6m/s由西向东运动,乙物体以速度2m/s由东向西运动,碰撞后两物体都沿各自原运动方向的反方向运动,速度大小都是4m/s。求:
(1)甲、乙两物体质量之比;
(2)通过计算说明这次碰撞是弹性碰撞还是非弹性碰撞。
参考答案:(1)3/5
(2)弹性碰撞
本题解析:
本题难度:一般
5、计算题 如图所示,物体A、B的质量分别是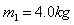 和
和 ,用轻弹簧相连结放在光滑的水平面上,物体B左侧与竖直墙相接触。另有一个物体C从t=0时刻起以一定的速度向左运动,在t=0.5s时刻与物体A相碰,碰后立即与A粘在一起不再分开。物体C的v-t图象如图所示。试求:
,用轻弹簧相连结放在光滑的水平面上,物体B左侧与竖直墙相接触。另有一个物体C从t=0时刻起以一定的速度向左运动,在t=0.5s时刻与物体A相碰,碰后立即与A粘在一起不再分开。物体C的v-t图象如图所示。试求:
(1)物块C的质量m3;
(2)在5.0s到15s的时间内物块A的动量变化的大小和方向。
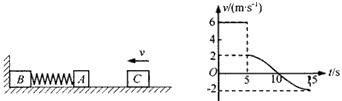
参考答案:解:(1)根据图象可知,物体C与物体A相碰前的速度为:v1=6m/s
相碰后的速度为:v2=2m/s
根据动量守恒定律得: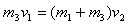
解得:m3=2.0kg
(2)规定向左的方向为正方向,在第5.0s和第15s末物块A的速度分别为:v2=2m/s,v3=-2m/s
所以物块A的动量变化为: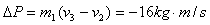
即在5.0s到15s的时间内物块A动量变化的大小为:16kg·m/s,方向向右
本题解析:
本题难度:一般