微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、简答题 为了缩短下楼的时间,消防队员往往抱着竖直杆从楼上直接滑下,先以尽可能大的加速度沿杆做匀加速直线运动,再以尽可能大的加速度沿杆做匀减速直线运动.假设一名质量为m=65kg训练有素的消防队员(可视为质点),在沿竖直杆无初速下滑至地面的过程中,重心共下移了s=11.4m,已知该队员与杆之间的最大滑动摩擦力可达f=975N,队员着地时的速度不能超过V1=6m/s,重力加速度为10m/s2,忽略空气对队员的作用力.求
(1)该队员下落过程中的最大速度.
(2)该队员下落过程中的最短时间.
参考答案:(1)队员先做自由落体运动,则有:
V2=2gh…(1)
当速度达到v后开始做匀减速直线运动
V2-v12=2ah…(2)
由牛顿第二定律
f-mg=ma?
解得:a=5m/s…..(3)
又?s=h1+h2…(4)
由(1)(2)(3)(4)式解得
V=10m/s
(2)队员下滑过程中有.
V=gt1?
解得:t1=1s…(5)
而V=V1+at2?
解得t2=0.8s…(6)
运动过程中最短时间t
t=t1+t2…(7)
由(5)(6)(7)得
t=1.8s
答:(1)该队员下落过程中的最大速度为10m/s.
(2)该队员下落过程中的最短时间为1.8s.
本题解析:
本题难度:一般
2、计算题 A、B两辆汽车在笔直的公路上同向行驶。当B车在A车前84 m处时开始计时,此时B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零,A车一直以20 m/s的速度做匀速运动,从记时开始经过12 s后两车相遇。问B车加速行驶的时间是多少?
参考答案:解:设A车的速度为vA,B车加速行驶时间为t,两车在t0时相遇。则有
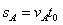 ?①
?①
 ?②
?②
式中,t0=12s,sA、sB分别为A、B两车相遇前行驶的路程
依题意有 ③,式中s=84 m
③,式中s=84 m
由①②③式得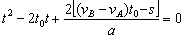 ④
④
代入题给数据vA=20m/s,vB=4m/s,a=2m/s2
有 ⑤,式中的单位为s
⑤,式中的单位为s
解得t1=6 s,t2=18 s ⑥
t2=18s不合题意,舍去
因此,B车加速行驶的时间为6 s ⑦
本题解析:
本题难度:困难
3、简答题 一个做匀加速直线运动的质点,初速度为0.5m/s,在第9秒内的位移比第8秒内的位移多1m,求:
(1)质点的加速度;
(2)质点在9s内通过的位移.
参考答案:(1)第9s内的位移比第8s的位移多△s=aT2,
代入数据得:a=1m/s2;
(2)根据位移公式s=v0t+12at2,
解得s=45m.
答:(1)质点的加速度a=1m/s2;
(2)质点在9s内通过的位移为45m.
本题解析:
本题难度:一般
4、计算题 (12分)一辆汽车从静止开始匀加速开出,然后保持匀速运动,最后匀减速运动,直到停止,下表给出了不同时刻汽车的速度:
时刻/s
| 1.0
| 2.0
| 3.0
| 5.0
| 7.0
| 9.5
| 10.5
|
速度/m·s-1
| 3
| 6
| 9
| 12
| 12
| 9
| 3
|
(1)汽车做匀速运动时的速度大小是否为12 m/s?求汽车做加速运动时的加速度和减速运动时的加速度大小?
(2)汽车从开出到停止总共经历的时间是多少?
(3)汽车通过的总路程是多少?
参考答案:(1)是;3m/s2;6m/s2;(2)11s;(3)96m;
本题解析:(1)由表中数据可知,汽车匀速运动的速度大小是12m/s?1分
由加速度定义可得加速阶段: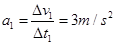 ? 2分
? 2分
减速阶段:  ?2分
?2分
(2)自10.5s时刻到汽车停止用时: 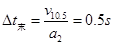 ?1分
?1分
故汽车经历的总时间为: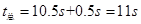 ? 1分
? 1分
(3)汽车的加速时间: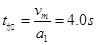 ? 1分
? 1分
减速时间为: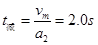 ? 1分
? 1分
由运动学公式可知汽车行驶的总路程为:
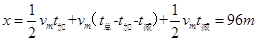 ? 3分
? 3分
本题难度:一般
5、简答题 如图所示,B为位于水平地面上的质量为M的长方形空心盒子,盒内存在着竖直向上场强大小为E=
的匀强电场.A为位于一定高度处的质量为m、带电荷量为+q的小球,且M=2m,盒子与地面间的动摩擦因数μ=0.2,盒外没有电场.盒子的上表面有一些略大 于小球直径的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v1=6m/s的速度向右滑行.已知盒子通过电场对小球施加的作用力与小球通过电场对盒子施加的作力大小相等方向相反.设盒子足够长,取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
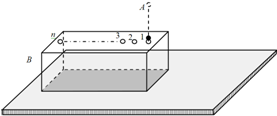
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.
参考答案:(1)A在盒子内运动时,qE-mg=ma
E=2mgq
由以上两式得 a=g=10m/s2?
A在盒子内运动的时间t1=2va=0.2s
A在盒子外运动的时间t2=2vg=0.2s
A从第一次进入盒子到第二次进入盒子的时间T=t1+t2=0.4s
(2)小球在盒子内运动时,盒子的加速度a1=μ(Mg+qE)M=4m/s2
小球在盒子外运动时,盒子的加速度a2=μMgM=2m/s2
小球运动一个周期盒子减少的速度为△v=a1t1+a2t2=4×0.2+2×0.2=1.2m/s
从小球第一次进入盒子到盒子停下,小球运动的周期数为n=v1△v=61.2=5
要保证小球始终不与盒子相碰,小孔数至少为2n+1个,即11个.
(3)小球第一次在盒内运动的过程中,盒子前进的距离为s1=v1t1-12a1t21=1.12m
小球第一次从盒子出来时,盒子的速度v2=v1-a1t1=5.2m/s
小球第一次在盒外运动的过程中盒子前进距离s2=v2t2-12a2t22=1m
小球第二次进入盒子时,盒子的速度v3=v2-a2t2=4.8m/s
小球第二次在盒子内运动的过程中,盒子前进的距离为s3=v3t1-12a1t21=0.88m
小球第二次从盒子出来时,盒子的速度v4=v3-a1t1=4m/s
小球第二次在盒外运动的过程中,盒子前进的距离为s4=v4t2-12a2t22=0.76m
分析上述各组数据可知,盒子在每个周期内通过的距离为一等差数列,公差d=0.12m.且当盒子停下时,小球恰要进入盒内,最后0.2s内盒子通过的路程为0.04m.所以从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程为s=n(s1+s10)2=10(1.12+0.04)2=5.8m
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间0.4s
(2)盒子上至少要开11个小孔,才能保证小球始终不与盒子接触
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程5.8m
本题解析:
本题难度:一般