微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
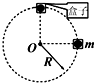
1、选择题 如图所示,质量为m的小球置于立方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间作用力恰为mg,则( )
A.该盒子做匀速圆周运动的周期一定小于π
B.该盒子做匀速圆周运动的周期一定等于π
C.盒子在最低点时盒子与小球之间的作用力大小可能小于3mg
D.盒子在最低点时盒子与小球之间的作用力大小可能大于3mg
|
参考答案:AB、要使在最高点时盒子与小球之间恰好为mg,则盒子顶部对小球必然有向下的弹力mg,则有mg+mg=mv2R,解得该盒子做匀速圆周运动的速度v=
本题解析:
本题难度:一般
2、简答题 图1所示为一根竖直悬挂的不可伸长的轻绳,下端栓一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动.在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图2所示.已知子弹射入的时间极短,且图2中t=0为A、B开始以相同速度运动的时刻.根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
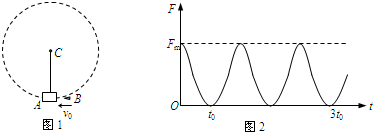
参考答案:由图2可直接看出,A、B一起做周期性运动,运动周期为T=2t0.用m、m0分别表示A、B的质量,l表示绳长,v1、v2分别表示它们在圆周最低、最高点的速度,F1、F2分别表示运动到最低、最高点时绳的拉力大小;
子弹射入木块过程,根据动量守恒定律,有
m0v0=(m+m0)v1? ①
根据牛顿定律有:
最低点? F1-(m+m0)g=(m+m0)v21l? ②
最高点? F2+(m+m0)g=(m+m0)v22l? ③
由机械能守恒又有:
(m+m0)g?(2l)=12(m+m0)v12-12(m+m0)v22? ④
由图2知,F2=0,F1=Fm,由以上各式解得,反映系统本身性质的物理量是
木块质量? m=Fm6g-m0
细线长度? l=36m20v205F2mg
以最低点所在的水平面为参考平面,系统总机械能是
E=12(m+m0)v12 ⑤
解得
E=3m20v20gFm
故可以求出A的质量为Fm6g-m0,细线长度为36m20v205F2mg,A、B一起运动过程中的守恒量为机械能,以最低点所在的水平面为参考平面,总机械能为3m20v20gFm.
本题解析:
本题难度:一般
3、计算题 一质量为2000 kg的汽车,行驶到一座半径为40m的圆弧形拱桥顶端时,汽车运动速度为8m/s。求此时汽车对桥面的压力的大小(g=10m/s2)。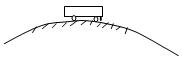
参考答案:圆弧形拱桥,向心力
本题解析: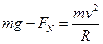 ? ······3分; ? ······3分;
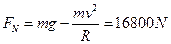 ? ·······2分; ? ·······2分;
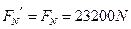 ? ·····1分; ? ·····1分;
本题难度:简单
4、选择题 甲、乙两个物体都做匀速圆周运动,其质量之比为1∶2,转动半径之比为1∶2,在相同时间里甲转过60°角,乙转过45°角。则它们的向心力之比为
[? ]
A.1∶4
B.2∶3
C.4∶9
D.9∶16
参考答案:C
本题解析:
本题难度:一般
5、选择题 甲乙两物体做匀速圆周运动,甲物体的质量和它的转动半径均为乙物体的一半,当甲物体转过60°时,乙物体只转过45°,则甲、乙两物体所受到的向心力之比为( )
A.9:64
B.2:3
C.4:9
D.9:16
参考答案:由题:当甲物体转过60°时,乙物体只转过45°时,根据角速度的定义ω=△θ△t得到:ω1:ω2=4:3,
又根据向心力的公式Fn=mω2r得到向心力之比F1:F2=m1ω12r1:m2ω22r2=4:9
故选C
本题解析:
本题难度:一般
|