微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图,一带电小球用丝线悬挂在沿水平方向的匀强电场中,当小球静止后把悬线烧断,则小球在电场中将做? (? )
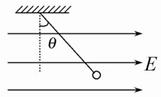
A.自由落体运动
B.曲线运动
C.沿着悬线的延长线做匀加速直线运动
D.变加速直线运动
参考答案:C
本题解析:开始时小球受力平衡,受电场力、重力、绳子拉力,悬线烧断后,重力、电场力不变,绳子拉力为零,小球受到的合力方向沿悬线的延长线方向,大小为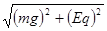 且保持不变,由牛顿第二定律可知,小球做初速度为零的匀加速直线运动,所以只有选项C正确。
且保持不变,由牛顿第二定律可知,小球做初速度为零的匀加速直线运动,所以只有选项C正确。
本题难度:一般
2、计算题 如图甲所示,M和N是相互平行的金属板,OO1O2为中线,O1为板间区域的中点,P是足够大的荧光屏。带电粒子连续地从O点沿OO1方向射入两板间。
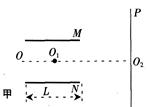
(1)若在两板间加恒定电压U,M和N相距为d,板长为L(不考虑电场边缘效应),入射粒子是电量为e、质量为m的电子,求打在荧光屏P上偏离点O2最远的粒子的动能
(2)若在两板间加如图乙所示的交变电压u,M和N相距为d,板长为L(不考虑电场边缘效应)。入射粒子是电量为e、质量为m的电子。某电子在t0=L/4v0时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件
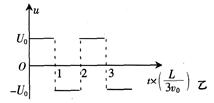
参考答案:(14分)
(1)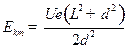 ?(8分)
?(8分)
(2)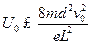 ?(6分)
?(6分)
本题解析:略
本题难度:一般
3、计算题 有一平行板电容器,内部为真空,两个电极板的间距为 ,极板的长为L,极板间有一均匀电场,U为两极板间的电压,电子从极板左端的正中央以初速
,极板的长为L,极板间有一均匀电场,U为两极板间的电压,电子从极板左端的正中央以初速 射入,其方向平行于极板,并打在极板边缘的D点,如图甲所示。电子的电荷量用e表示,质量用
射入,其方向平行于极板,并打在极板边缘的D点,如图甲所示。电子的电荷量用e表示,质量用 表示,重力不计。回答下面各问题(用字母表示结果)
表示,重力不计。回答下面各问题(用字母表示结果)

(1)求电子打到D点的动能;
(2)电子的初速V0至少必须大于何值,电子才能飞出极板?
(3)若极板间没有电场,只有垂直进入纸面的匀强磁场,其磁感应强度为B,电子从极板左端的正中央以平行于极板的初速 射入,如图乙所示,则电子的初速
射入,如图乙所示,则电子的初速 为何值,电子才能飞出极板?
为何值,电子才能飞出极板?
参考答案:(1) ?(2)
?(2)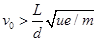 ?
?
(3)两种可能:①电子从左边出,
②电子从右边出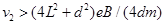
本题解析:(1)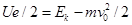 ?(2分)
?(2分)
 ?(1分)
?(1分)
(2)设电子刚好打到极板边缘时的速度为V,则 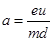 ?(1分)
?(1分)
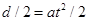 (2分)
(2分)
 ?(2分)
?(2分)
解得 ?(1分)
?(1分)
要逸出电容器外必有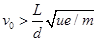 ?(1分)
?(1分)
(3)有两种情况
①电子从左边出,做半圆周运动其半径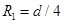 ?(1分)
?(1分)
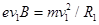 ?(1分)
?(1分)
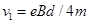 ?(1分)
?(1分)
电子避开极板的条件是 ?(1分)
?(1分)
②电子从右边出, ?
?
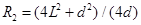 ?(1分)
?(1分)
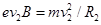 ?(1分)
?(1分)
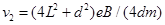 ?(1分)
?(1分)
电子避开极板的条件是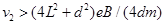 ?(1分)
?(1分)
本题难度:简单
4、计算题 两平行金属板A、B水平放置,一个质量m=5×10-6kg的带电微粒以υ0=2m/s的水平初速度从两板正中央位置 射入电场,如图所示,A、B两板间的距离d=4cm,板长L=10cm。
射入电场,如图所示,A、B两板间的距离d=4cm,板长L=10cm。
(1)当A、B间的电压UAB=1000V时,微粒恰好不偏转,沿图中直线射出电场,求该粒子的电量。
(2)令B板为电势零点,A板电势高于B板电势,欲使该微粒射出偏转电场,求AB板电势差的最大值和最小值。

参考答案:(1)当U AB=1000V时,重力跟电场力平衡,微粒沿初速方向做匀速直线运动,由qUAB/d=mg得:q=mgd/UAB=2×10-9C。因重力方向竖直向下,故电场力方向必须竖直向上。又场强方向竖直向下(UAB>0),所以微粒带负电。————(4分)
AB=1000V时,重力跟电场力平衡,微粒沿初速方向做匀速直线运动,由qUAB/d=mg得:q=mgd/UAB=2×10-9C。因重力方向竖直向下,故电场力方向必须竖直向上。又场强方向竖直向下(UAB>0),所以微粒带负电。————(4分)
(2)当qE>mg时,带电微粒向上偏。设微粒恰好从上板右边缘飞出时AB板电势差为UAB。此时,微粒在水平方向做匀速 运动,在竖直方向作加速度a=qUAB/(md)-g的匀加速运动,由d/2=at2/2 和t=L/υ0得UAB1=(mυ02d2+mgdL2)/qL2=2600V。————(8分)
运动,在竖直方向作加速度a=qUAB/(md)-g的匀加速运动,由d/2=at2/2 和t=L/υ0得UAB1=(mυ02d2+mgdL2)/qL2=2600V。————(8分)
当qE<mg时,带电微粒向下偏转,竖直方向加速度a=g-qUAB2/md,同理可得UAB2=600V。所以,要使微粒射出偏转电场, UAB最大值为2600V,最小值为600V。————(8分)
本题解析:略
本题难度:简单
5、计算题 如图所示,平行板电容器竖直放置在水平绝缘地板上,一个带电质点质量为m=0.10×10- 3kg,电荷量为q=" -" 2.0×10- 4C,从电容器中心线上某点由静止开始自由下落,下落了h1=0.80m后进入匀强电场,又下落了h2=1.0m后到达水平绝缘地板。落地点在两板中心O点左侧s=20cm处(未碰板)。g取10m/s2。求:
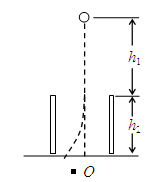
(1)带电质点在空中运动的时间;
(2)电容器中匀强电场的场强E的大小和方向。
参考答案:(1)0.6s (2)5v/m , 电场强度的方向为水平向右
本题解析:(1)带电质点在空中的运动可分解为竖直方向和水平方向的运动,在水平方向进入电场后受到的电场力为水平向左(暂不讨论),在竖直方向带电质点始终只受重力的作用,其做自由落体运动,根据运动合成分解的原理分运动的时间与合运动的时间相同,可以通过求解竖直方向运动的时间来确定合运动的时间,设带电质点在空中下落的时间为t,则有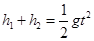 ①,将数值代入①式可得t=0.6s;
①,将数值代入①式可得t=0.6s;
(2)设带电质点在进入电场之前下落的时间为t1,带电质点在电场中运动的时间为t2,则有t2="t-" t1,在竖直方向带电质点始终只受重力的作用,其做自由落体运动,故由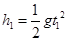 有
有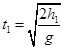 =0.4(s),则有t2="t-" t1=0.6-0.4=0.2(s),在水平方向进入电场后受到的电场力为水平向左,研究带电质点进入电场后水平方向的运动为初速为0的匀加速运动,设其水平方向的加速度为a,则有
=0.4(s),则有t2="t-" t1=0.6-0.4=0.2(s),在水平方向进入电场后受到的电场力为水平向左,研究带电质点进入电场后水平方向的运动为初速为0的匀加速运动,设其水平方向的加速度为a,则有 ③,水平方向的加速度为电场力的作用所产生故由牛顿第二运动定律有
③,水平方向的加速度为电场力的作用所产生故由牛顿第二运动定律有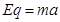 ④,联立③④代入数值有E=5V/m,电场力为水平向左带电质点来负电荷,负电荷所受电场力的方向与电场强度的方向相反,故电场强度的方向为水平向右。
④,联立③④代入数值有E=5V/m,电场力为水平向左带电质点来负电荷,负电荷所受电场力的方向与电场强度的方向相反,故电场强度的方向为水平向右。
本题难度:一般
It is better to please a fool than to anget him. 若惹蠢人生气,不如使他欢喜。