微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 如图所示,半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁场方向垂直于纸面向里,匀强磁场的磁感应强度为B,圆筒形场区的边界由弹性材料构成。一个质量为m.电荷量为q的正离子(不计重力)以某一速度从筒壁上的小孔M进入筒中,速度方向与半径成θ=30°夹角,并垂直于磁场方向。离子和筒壁的碰撞无能量和电荷量的损失.若选择合适的进入速度,离子可以从M孔射出。问:
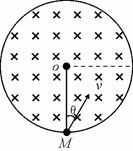
(1)离子的速度多大时,离子可以在最短的时间内返回M孔最短的时间是多少?
(2)如果离子与筒壁发生两次碰撞后从M孔射出,离子的速率是多大?从进入圆筒到返回M孔经历的时间是多少?
参考答案:(1) 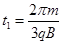 ?(2)
?(2)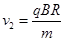 ?
?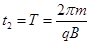
本题解析:(1)离子要在最短的时间内返回M孔,离子只能与圆筒碰撞一次,据此画出离子的运动轨迹如图所示,碰撞点在过M点的直径的另一端N。设离子在磁场中的轨迹半径为r,速率为V1.根据向心力公式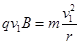 ,①结合图中的几何关系可得r=2R,②解得离子的速率
,①结合图中的几何关系可得r=2R,②解得离子的速率 ,③离子在磁场中走过的每段圆弧对应的圆心角
,③离子在磁场中走过的每段圆弧对应的圆心角 =60°,④经历的时间
=60°,④经历的时间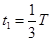 ,⑤即
,⑤即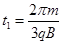 .⑥
.⑥
(2)离子与筒壁发生两次碰撞后从M孔射出,根据对称性画出离子的运动轨迹如图所示。
结合图中的几何关系可得r=R,?⑦
则离子的速率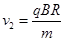 ,?⑧
,?⑧
离子在磁场中走过的每段圆弧对应的圆心角 ′=120°,?⑨
′=120°,?⑨
经历的时间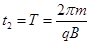 。?⑩
。?⑩
 ?
?
本题难度:一般
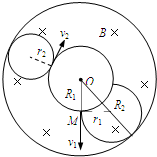
2、简答题 未来人类要通过可控热核反应取得能源,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内.约束的办法有多种,其中技术上相对较成熟的是用磁场约束核材料,称为“托卡马克”装置.如图所示为这种装置的简化模型:有环形边界的匀强磁场(b区域)围着磁感应强度为零的圆形a区域,a区域内的离子向各个方向运动,离子的速度只要不超过某值,就不能穿过环形磁场的外边界而逃逸,从而被约束.
设环形磁场的内半径R1=0.50m,外半径R2=1.0m,若磁场的磁感应强度B=1.0T,被约束的离子比荷
=4.0×107C/kg.
(1)完成核反应方程:He+H→He+______.
(2)若a区域中沿半径0M方向射入磁场的离子不能穿出磁场的外边界,粒子的速度不能超过多大?
(3)若要使从a区域沿任何方向射入磁场的速率为2×107m/s的离子都不能越出磁场的外边界,则b区域磁场的磁感应强度B至少要有多大?
参考答案:
(1)核反应方程中,质量数守恒,核电荷数守恒,所以有:
?32He+?21H→?42He+?11H
(2)速度越大,轨迹圆半径越大,要使沿0M方向运动的离子不能穿越磁场,则其在环形磁场内的运动轨迹圆中最大者与磁场外边界圆相切?
设轨迹圆的半径为r1,则:r21+R21=(R2-r1)2?
代入数据解得?r1=0.375m?
设沿该圆运动的离子速度为v1,qv1B=mv21r1
即?v1=Bqr1m
代入数据得v1=1.5×107m/s?
(3)设离子以v2的速度沿与内边界圆相切的方向射入磁场且轨道与磁场外圆相切时,则以该速度沿各个方向射入磁场区的离子都不能穿出磁场边界?(也可用图形表达?1分)
设轨迹圆的半径为r2,则r2=R2-R12=0.25m?
设磁场的磁感强度为B1,由?B1=mv2qr2
代入数据得?B′=2.0T?
答:(1)?32He+?21H→?42He+?11H
(2)速度最大为v1=1.5×107m/s?
(3)则b区域磁场的磁感应强度B至少要有2.0T.
本题解析:
本题难度:一般
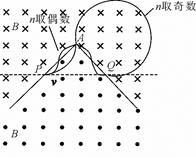
3、选择题 如图所示,在I、II两个区域内存在磁感应强度均为B的匀强磁场,磁场方向分别垂直于纸面向 外和向里,AD、AC边界的夹角∠DAC=300,边界AC与 边界MN平行,II区域宽度为d。质量为m、电荷量为十q的粒子可在边界AD上的不同点射人,入射速度垂直AD且垂直磁场,若入射速度大小为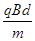 ?,不计粒子重力,则
?,不计粒子重力,则
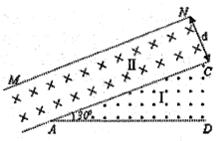
A.粒子在磁场中的运动半径为
B.粒子距A点0.5d处射入,不会进入II区
C.粒子距A点1.5d处射入,在I区内运动的时间为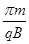
D.能够进入II区域的粒子,在II区域内运动的最短时间为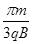
参考答案:CD
本题解析:粒子在磁场中做圆周运动的向心力由洛伦兹力提供,则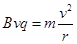 ,解得
,解得 ,选项A 错误;粒子距A点0.5d处射入时,圆心在AD上距离A点为1.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子不会进入II区,选项B错误;粒子距A点1.5d处射入,圆心在AD上距离A点为2.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子在I区将做半个圆周运动而射出,所以运动的时间为
,选项A 错误;粒子距A点0.5d处射入时,圆心在AD上距离A点为1.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子不会进入II区,选项B错误;粒子距A点1.5d处射入,圆心在AD上距离A点为2.5d,由几何知识可知,此圆周不会与AC边界相切,故粒子在I区将做半个圆周运动而射出,所以运动的时间为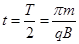 ;因为能够进入II区域的粒子的运动半径等于在I区域内的运动半径,若在II区域内运动的最短,则需弦长最短,而最短的弦长为d,此弦长所对圆心角为
;因为能够进入II区域的粒子的运动半径等于在I区域内的运动半径,若在II区域内运动的最短,则需弦长最短,而最短的弦长为d,此弦长所对圆心角为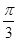 ,所以运动的时间为
,所以运动的时间为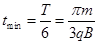 ,选项D 正确。
,选项D 正确。
本题难度:一般
4、计算题 如图所示,在第二象限和第四象限的正方形区域内分别存在着匀强磁场,磁感应强度均为B,方向相反,且都垂直于xOy平面.一电子由P(-d,d)点,沿x轴正方向射入磁场区域Ⅰ.(电子质量为m,电荷量为e,sin 53°= )
)
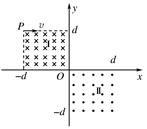
(1)求电子能从第三象限射出的入射速度的范围.
(2)若电子从 位置射出,求电子在磁场 Ⅰ 中运动的时间t.
位置射出,求电子在磁场 Ⅰ 中运动的时间t.
(3)求第(2)问中电子离开磁场Ⅱ时的位置坐标.
参考答案:(1)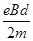 <v<
<v<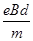 (2)
(2)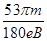 (3)
(3)
本题解析:(1)电子能从第三象限射出的临界轨迹如图甲所示.电子偏转半径范围为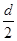 <r<d
<r<d

由evB=m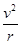 得v=
得v=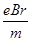
故电子入射速度的范围为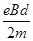 <v<
<v<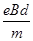 .
.
(2)电子从 位置射出的运动轨迹如图乙所示.设电子在磁场中运动的轨道半径为R,则R2=
位置射出的运动轨迹如图乙所示.设电子在磁场中运动的轨道半径为R,则R2=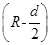 2+d2
2+d2
解得R=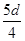
则∠PHM=53°
由evB=mR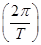 2解得T=
2解得T=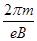
电子在磁场Ⅰ中运动的时间t= T=
T=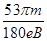 .
.
(3)如图乙所示,根据几何知识,带电粒子在射出磁场区域Ⅰ时与水平方向的夹角为53°,在磁场区域Ⅱ位置N点的横坐标为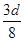 .
.
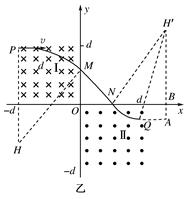
由△NBH′可解得NB的长度等于d,则QA=d-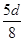
由勾股定理得H′A=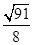 d,H′B=Rcos 53°=
d,H′B=Rcos 53°=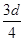
所以电子离开磁场Ⅱ的位置坐标为 .
.
本题难度:一般
5、选择题 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16( )
A.该原子核发生了α衰变
B.反冲核沿小圆做逆时针方向运动
C.原静止的原子核的原子序数为15
D.沿大圆和沿小圆运动的粒子的周期相同
