1、计算题  有一倾角为θ的斜面，其底端固定一挡板M，另有三个木块A、B和c，它们的质量分别为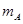==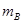"m," 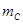=3m，它们与斜面间的动摩擦因数都相同.其中木块A连接一轻弹簧放于斜面上，并通过轻弹簧与挡板M相连，如图所示.开始时，木块A静止在P处，弹簧处于自然伸长状态.木块B在Q点以初速度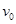)向下运动，P、Q间的距离为L.已知木块B在下滑过程中做匀速直线运动,与木块A相撞后立刻一起向下运动，但不粘连，它们到达一个最低点后又向上运动，木块B向上运动恰好能回到Q点.若木块A仍静止于P点，木块C从Q点开始以初速度向下运动，经历同样过程，最后木块C停在斜面上的R点，求P、R间的距离L’的大小.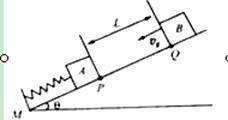

参考答案：

本题解析：木块B下滑做匀速直线运动，有?
B和A相撞前后，总动量守恒，，所以?
设两木块向下压缩弹簧的最大长度为s，两木块被弹簧弹回到P点时的速度为，则
?
两木块在P点处分开后，木块B上滑到Q点的过程：?
木块C与A碰撞前后，总动量守恒，则，所以?
设木块C和A压缩弹簧的最大氐度为S’，两木块被弹簧弹回到P点时的速度为，则
?
木块C与A在P点处分开后，木块C上滑到R点的过程：?
在木块压缩弹簧的过程中，重力对木块所做的功与摩擦力对木块所做的功大小相等，因此弹簧被压缩而具有的最大弹性势能等于开始压缩弹簧时两木块的总动能。因此，木块B和A压缩弹簧的初动能，木块C与A压缩弹簧的初动能
，即=?因此，弹簧前后两次的最大压缩量相等，即s=s’
综上，得?
点评：明确物理过程，利用动量守恒定律结合能的转化和守恒定律列式求解，是解决力学综合题的关键。

本题难度：一般

2、选择题  如图，木板A放在水平地面上，小物块B通过轻弹簧与A的左侧档板P 连接，A与B、A与地面之间均粗糙。开始时弹簧处于原长，B位于A上的O点。现将B拉至C点由静止释放向左运动，到达某点时速度为零(上述过程中A一直保持静止)，则此时(? )

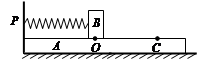
A．B所受的摩擦力可能为零? B．A所受的摩擦力不可能为零
C．B可能位于O点的左侧? D．B不可能位于O点的右侧

参考答案：AC

本题解析：物块在运动过程中弹簧弹力和滑动摩擦力做功，根据功的定义式可知，克服滑动摩擦力做的功为μmgs，弹簧拉至C处克服弹簧弹力做的功即储蓄的弹性势能为，由于弹簧的劲度系数k、A与B之间的动摩擦因数μ以及物块的质量m都不知道，因此无法确定最终物块停在何处，即s与x的大小，故选项A、C正确；选项B、D错误。

本题难度：一般

3、选择题  如图所示，小球从高处下落到竖直放置的轻弹簧上，从小球接触弹簧到将弹簧压缩至最短的过程中(弹簧一直保持竖直)?（?）

A．弹簧的弹性势能先增大后减小
B．弹簧的弹性势能增加量大于小球重力势能减少量
C．小球的动能一直在减小
D．小球的机械能守恒

参考答案：B

本题解析：略

本题难度：简单

4、计算题  在h高处，以初速度v0向水平方向抛出一个小球，不计空气阻力，小球着地时速度大小为多少？

参考答案：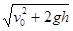

本题解析：小球下落为曲线运动，在小球下落的整个过程中，对小球应用动能定理，有
，
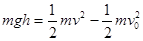解得小球着地时速度的大小为?。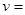

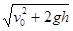本题难度：简单

5、选择题  如图有三个斜面1，2，3斜面1与2底边相同，斜面2和3高度相同，同一物体与三个斜面的摩擦数相同，当物体分别沿三个斜面从顶端由静止下滑到底端时，下列说法正确的是（?）

A．三种情况下物体损失的机械能△E3>△E2>△E1
B．三种情况下摩擦产生热量Q1＝Q2<Q3
C．到达底端的速度
D．运动时间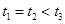

参考答案：B

本题解析：设斜面夹角为θ，1.2斜面摩擦力做功等于损失的机械能△E=umgcosθ×h/sinθ
=umg h/tanθ= umgs,所以△E2=△E1，A错；
2和3比较△E=umgh/ tanθ,, θ角越大tanθ越大，△E越小，所以△E3>△E2，B对；
根据动能定理mgh- umgs=mv^2/2-0,,C错；


,

,D错

本题难度：简单