微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,在重力加速度为g的空间,有一带电量为+Q的场源电荷置于O点,B、C为以O为圆心,半径为R的竖直圆周上的两点,A、B、O在同一竖直线上,AB=R,O、C在同一水平线上.现在有一质量为m,电荷量为-q的有孔小球,沿光滑绝缘细杆AC从A点由静止开始下滑,滑至C点时的速度的大小为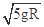 ,下列说法正确的是
,下列说法正确的是
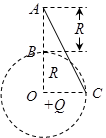
A.从A到C小球做匀加速直线运动?
B.从A到C小球的机械能守恒
C.A、C两点间的电势差为UAC=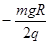
D.若将小球从A点沿ABO自由释放,则下落到B点时的速度大小为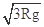
参考答案:CD
本题解析:小球所受电场力在变化,加速度在变化,物体做变加速运动,所以A错误。电场力做正功,电势能减少,机械能增加,所以B错误。从A到C,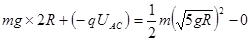 ,所以
,所以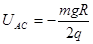 ;从A到B,
;从A到B,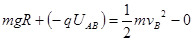 ,且
,且 ,所以
,所以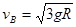 。故选CD
。故选CD
点评:难度中等,再利用W=qU计算电场力做功问题时,要注意W和U的下脚标,明确重力、电场力做功只与初末位置有关,与路径无关
本题难度:一般
2、计算题 如图所示,水平固定放置的两根平行光滑导轨MN、PQ,两导轨间距L=0.50 m,导轨间接有电阻R=0.50Ω.一导体棒ab垂直跨放在导轨上,现在力F的作用下在导轨上匀速滑动。已知除电阻R外,导体棒ab和导轨的电阻都可忽略不计,匀强磁场垂直框架平面向里,磁感应强度,B=0.40 T.导轨足够长.当ab以v=4.0 m/s的速度向右匀速滑动时,(g=10m/s2)
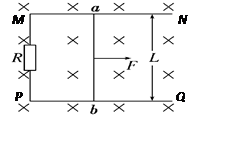
求:(1)ab棒中产生的感应电动势大小;
(2)维持导体棒ab做匀速运动的外力F的大小.
参考答案:(1)0.8V(2)0.32N
本题解析: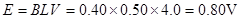 ?(3分)
?(3分)
 ?(3分)
?(3分)
 ?(3分)
?(3分)
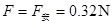 ?(3分)
?(3分)
点评:明确切割磁感线的导体相当于电源,根据E=BLV求解,把此类问题转化为闭合电路问题,由欧姆定律求得电流,求解此类问题根据以上思路可轻松求解
本题难度:一般
3、计算题 如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场,在第四象限,存在沿y轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为m、电量为q的带电质点,从y轴上y?=?h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x?=?–?2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y?=?–?2h处的P3点进入第四象限。已知重力加速度为g。求:
(1)带电质点到达P2点时速度的大小和方向;
(2)第三象限空间中电场强度和磁感应强度的大小;
(3)带电质点在第四象限空间运动过程中最小速度的大小和方向。

参考答案:解:(1)质点从P1到P2,由平抛运动规律
h= ,v0=
,v0= ,vy=gt
,vy=gt
求出v = ,方向与x轴负方向成45°角?
,方向与x轴负方向成45°角?

(2)质点从P2到P3,重力与电场力平衡,洛仑兹力提供向心力
Eq=mg
Bqv=m
(2R)2=(2h)2+(2h)2
E= ,B=
,B=
(3)质点进入第四象限,水平方向做匀速直线运动,竖直方向做匀减速直线运动。当竖直方向的速度减小到0,此时质点速度最小,即v在水平方向的分量
vmin=vcos45°= ,方向沿x 轴正方向
,方向沿x 轴正方向
本题解析:
本题难度:一般
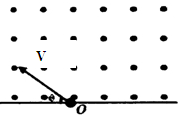
4、选择题 如图所示为一个有界的足够大的匀强磁场区域,磁场方向垂直纸面向里,一个不计重力的带正电的粒子以某一速率v垂直磁场方向从O点进入磁场区域,电子进入磁场时速度方向与边界夹角为θ,下列有关说法正确的是
A.若θ一定,速度v越大,粒子在磁场中运动时间越长
B.粒子在磁场中运动时间与速度v有关,与角θ大小无关
C.若速度v一定,θ越大,粒子在磁场中运动时间越长
D.粒子在磁场中运动时间与角度θ有关,与速度v无关
参考答案:CD
本题解析:粒子在磁场中的运动轨迹如图,由几何知识知,粒子离开磁场时转过的圆心角一定为2π-2θ;

若θ一定,则 ,所以粒子在磁场中的运动时间和速度无关;若速度v一定,θ越大,粒子在磁场中运动的时间越短选项AB错误,CD正确。
,所以粒子在磁场中的运动时间和速度无关;若速度v一定,θ越大,粒子在磁场中运动的时间越短选项AB错误,CD正确。
本题难度:一般
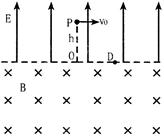
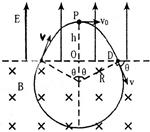
5、计算题 一宇宙人在太空(万有引力可以忽略不计)玩垒球。如图所示,辽阔的太空球场半侧为匀强电场,另半 侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场
侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场 方向与界面垂直,磁场方向垂直纸面向里,电场强度大小
方向与界面垂直,磁场方向垂直纸面向里,电场强度大小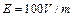 。宇宙人位于电场一侧距界面为
。宇宙人位于电场一侧距界面为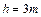 的
的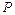 点,
点,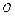 为
为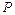 点至界面垂线的垂
点至界面垂线的垂 足,
足,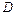 点位于纸面上
点位于纸面上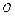 点的右侧,
点的右侧,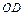 与磁场的方向垂直。垒球的质量
与磁场的方向垂直。垒球的质量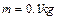 ,电量
,电量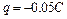 。宇宙人从
。宇宙人从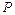 点以初速度
点以初速度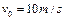 平行于界面投出垒球,要使垒球第一次通过界面时就击中
平行于界面投出垒球,要使垒球第一次通过界面时就击中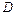 点,求:(计算结果保留三位有效数字)
点,求:(计算结果保留三位有效数字)
(1)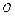 、
、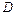 两点之间的距离。
两点之间的距离。
(2)垒球从抛出到第一次回到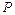 点的时间。
点的时间。
参考答案:(1)3.46m? (2)1.53s
本题解析:(1)设垒球在电场中运动的加速度大小为a,时间为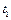 ,
,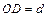 ,则:
,则:
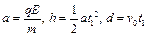 (3分,每式1分)
(3分,每式1分)
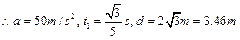
即O、D两点之间的距离为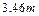 。(2分,没有保留三位有效数字的扣1分)
。(2分,没有保留三位有效数字的扣1分)
(2)垒球的运动轨迹如图所示。
由图可知,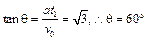 ,速度大小为:
,速度大小为: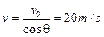 。(1分)
。(1分)
设垒球作匀速圆周运动半径为R,磁感应强度大小为B,则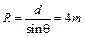 (1分)
(1分)
根据牛顿第二定律,有: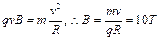 (1分)
(1分)
垒球在磁场中运动的时间为: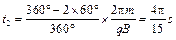 (2分
(2分 )
)
垒球从抛出到第一次回到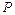 点的时间为:
点的时间为: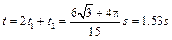 (2分,没有保留三位有效数字的扣1分)
(2分,没有保留三位有效数字的扣1分)
本题难度:简单