1、计算题  如图所示，AB为倾角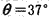的斜面轨道，轨道的AC部分光滑，CB部分粗糙。BP为圆心角等于143°半径R=1m的竖直光滑圆弧形轨道，两轨道相切于B点，P、0两点在同一竖茛 线上，轻弹簧一端固定在A点,另一 0由端在斜面上C点处，现有一质量m = 2kg的物块在外力作用下将弹簧缓慢压缩到D点后（不栓接）释放，物块经过C点后，从C点运动到B点过程中的位移与时间的关系为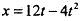（式中X单位是m,t单位是s），假设物块笫一次经过B点后恰能到达P点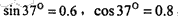，，g取10m/s2。试求：
(1) 若，试求物块从D点运动到C点的过程中，弹簧对物块所做的功；
(2) B、C两点间的距离x
(3) 若在P处安装一个竖直弹性挡板，小物块与挡板碰撞时间极短且无机械能损火，小物块与弹簧相互作用不损失机械能，试通过计箅判断物块在第一次与挡板碰撞后的运动过程中是否会脱离轨道？

参考答案：解：
（1）由，知，物块在C点速度为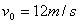
设物块从D点运动到C点的过程中，弹簧对物块所做的功为W，由动能定理得：

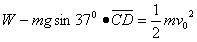
代入数据得：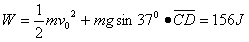
（2）由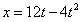知，物块从C运动到B过程中的加速度大小为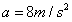
设物块与斜面间的动摩擦因数为，由牛顿第二定律得
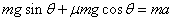代入数据解得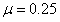
物块在P点的速度满足
物块从B运动到P的过程中机械能守恒
物块从C运动到B的过程中有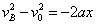
由以上各式解得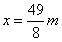
（3）假设物块第一次从圆弧轨道返回并与弹簧相互作用后，能够回到与O点等高的位置Q点，且设其速度为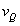，由动能定理得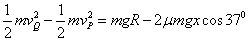
解得
可见物块返回后不能到达Q点，故物块在以后的运动过程中不会脱离轨道。

本题解析：

本题难度：困难

2、计算题  如图所示，由六根质量不计的导体棒组成一个人字形线圈，放在光滑绝缘水平面上，每根导棒长均为L=1m，线圈总电阻R=0.2Ω，将ad与a/d/用细线OO/拉住，e、f是两个质量都为m=0.1kg光滑转轴，四根倾斜导体棒与水平面成37 0角。人字形线圈在水平面投影区内有两块对称的区域，竖直向上的匀强磁场B穿过这两块区域。如图中阴影区域所示（ad与a/d/恰在磁场中），其他地方没有磁场。磁场按B=+0.5t 的规律变化，取sin37°＝0.6，cos37°＝0.8。求：?
（1）t=0时水平面对线圈ad边支持力的大小和此时通过线圈电流大小；
（2）经过多少时间线圈的ad边与a/d/边开始运动？
（3）若在磁场力作用下经过一段时间，当线圈中产生了Q=1.2J热量后线圈刚好能完全直立（即ad边与a/d/边并拢在一起），则在此过程中磁场对线圈总共提供了多少能量？
（4）若人形线圈从直立状态又散开，此时磁感强度为B0 =T且不再变化，则ad边与a/d/再次刚进入磁场时，通过线圈的电流为多大？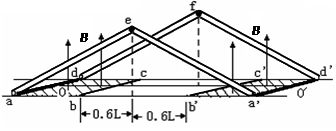

参考答案：（1）1A；（2）2s；（3）2J；（4）8.9A。

本题解析：（14分）
（1）对整个线圈以a/d/为转动轴，由力矩平衡有
N×2Lcos37o =2mg×Lcos37o
由上式得　N=mg=0.1×10N=1N　　　（1分）
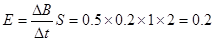V （1分）
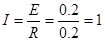A　　　　　　　　（1分）
（2）平衡刚被破坏时细线OO/中拉力为零，对半个线圈以e f为转动轴，由力矩平衡有
FA×Lsin37o ="N×L" cos37o?求得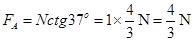（1分）
由　　　　　　　　　　　　　　　　　　　　　（1分）
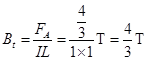得　　　　　　　　　　　　　　　（1分）
由关系式Bt=+0.5t　　得（1分）
（3）线圈由平衡被破坏到完全直立过程中机械能的增加量
ΔEP=2mgL(1－sin37o)=2×0.1×10×1×(1－0.6)J=0.8J　（1分）
磁场提供的能量 E=ΔEP+Q=（0.8+1.2）J=2J　　　（1分）
（4）人形线圈从直立状态又散开，ad边与a/d/再次刚进入磁场时，设两轴e、f的速度为v（方向竖直向下），ad边与a/d/边的速度大小为vx (方向水平)
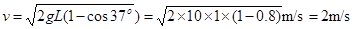由动能定理? 2mgL(1－cos37o)=2×mv2　　　　　　　　　　（1分）
　　（1分）
而vx =vctg37o=2×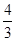=m/s　　　　　　　　　　　　　　　　（1分）
ad边与a/d/边每一条边的电动势Eˊ=B0Lvx =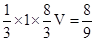V　　（1分）
线圈中的电流? Iˊ=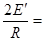　　　　　　（1分）

本题难度：简单

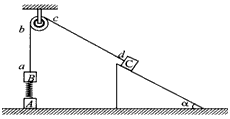
3、计算题  如图所示，在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上；B、C两物体通过细绳绕过轻质定滑轮相连，C放在固定的光滑斜面上。用手拿住C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行。已知A、B的质量均为m，C的质量为4m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态。释放C后它沿斜面下滑，A刚离开地面时，B获得最大速度，求：
（1）当物体A从开始到刚离开地面时，物体C沿斜面下滑的距离；
（2）斜面倾角α；
（3）B的最大速度vBm。

参考答案：解：（1）设开始时弹簧压缩的长度为xB，得： ①
设当物体A刚刚离开地面时，弹簧的伸长量为xA，得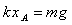： ②
当物体A刚离开地面时，物体B上升的距离以及物体C沿斜面下滑的距离为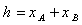： ③
由①②③式解得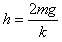： ④
（2）物体A刚刚离开地面时，以B为研究对象，物体B受到重力mg、弹簧的弹力kxA、细线的拉力T三个力的作用，设物体B的加速度为a，根据牛顿第二定律，对B有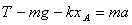： ⑤
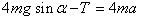对A有： ⑥
由②③两式得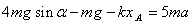： ⑦
当B获得最大速度时，有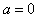： ⑧
由②⑦⑧式联立，解得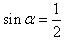： ⑨
所以： ⑩
（3）由于xA=xB，弹簧处于压缩状态和伸长状态时的弹性势能相等，弹簧弹力做功为零，且物体A刚刚离开地面时，B、C两物体的速度相等，设为vBm，由动能定理得：
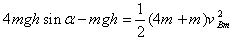?⑾
由①④⑩⑾式，解得：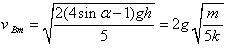

本题解析：

本题难度：困难

4、计算题  如图所示，一倾角为θ=37°的光滑斜面固定在地面上，斜面长度s0=3.0m，斜面底端有一垂直于斜面的固定挡板。在斜面顶端由静止释放一质量m=0.10kg的小物块。当小物块与挡板第一次碰撞后，能沿斜面上滑的最大距离s=0.75m。已知小物块第一次与挡板碰撞过程中从接触到离开所用时间为0.10s，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8。求：

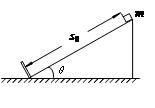
（1）小物块第一次与挡板碰撞前的速度大小；
（2）小物块第一次与挡板撞击过程中损失的机械能；
（3）小物块第一次与挡板撞击过程中受到挡板的平均作用力。

参考答案：：（1）6.0m/s?（2）1.35J?（3）F=9.60N，方向沿斜面向上

本题解析：（1）根据动能定理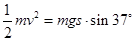，解得：v=6.0m/s；
（2）碰后物体的速度为v/,则根据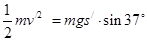，解得:v=3m/s；与挡板撞击过程中损失的机械能 。
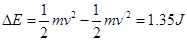（3）有动量定理，木块与板碰撞过程满足，解得：F=9.60N，方向沿斜面向上。

本题难度：一般

5、计算题  有一长为L的木块，质量为M，静止地放在光滑的水平面上，现有一质量为m的子弹（可视为质点）以初速度入射木块，若在子弹穿出木块的过程中，木块发生的位移为x，求子弹射出木块后，木块的速度和子弹的速度。（已知子弹在木块中受到的阻力恒为f）

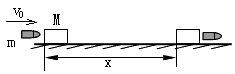
参考答案：解：在子弹和木块发生相互作用的过程中，对木块由动能定理有：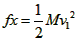
可解得：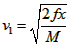
在子弹和木块发生相互作用的过程中，子弹发生的位移为：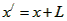
对子弹由动能定理有：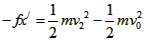
可解得：。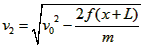

本题解析：

本题难度：困难