1、计算题  如图所示，一质量为M的平板车B放在光滑水平面上，在其右端放一质量为m的小木块A，m＜M，A、B间动摩擦因数为μ，现给A和B以大小相等、方向相反的初速度v0，使A开始向左运动，B开始向右运动，最后A不会滑离B，求：
（1）A、B最后的速度大小和方向；
（2）从地面上看，小木块向左运动到离出发点最远处时，平板车向右运动的位移大小。

参考答案：解：（1）由A、B系统动量守恒定律得：
Mv0－mv0=(M+m)v
所以v=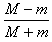v0，方向向右
（2）A向左运动速度减为零时，到达最远处，此时板车移动位移为s，速度为v′，则由动量守恒定律得：Mv0－mv0=Mv′ ①
对板车应用动能定理得：-μmgs=mv′2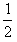－mv02 ②
联立①②解得：s=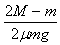v02

本题解析：

本题难度：一般

2、简答题  如图所示，在光滑桌面上放着长木板，其长度为L=1.0m，在长木板的左上端放一可视为质点的小金属块，它的质量和木板的质量相等，最初它们是静止的．现让小金属块以v0=2.0m/s的初速度开始向右滑动，当滑动到长木板的右端时，滑块的速度为v1=1.0m/s，取g=l0m/s2，求：
（1）小金属块刚滑到长木板右端时的速度大小v2及滑块与长木板间的动摩擦因数μ；
（2）小金属块刚滑到长木板右端时经历的时间t及长木板的位移大小x．

参考答案：（1）设小金属块和木板的质量均为m，
以小金属块与木板组成的系统为研究对象，
由动量守恒定律可得：mv0=mvl+mv2，
由能量守恒定律可得：12mv20-12mv21-12mv22=μmgL，
解得：v2=1m/s，μ=0.1；
（2）对木板由动能定理得：μmgx=12mv22-0，解得x=0.5m；
对木板，由牛顿第二定律得：μmg=ma，
由匀变速运动的速度公式得：v2=at，解得：t=1s；
答：（1）小金属块刚滑到长木板右端时的速度为1m/s，滑块与长木板间的动摩擦因数为0.1．
（2）小金属块刚滑到长木板右端时经历的时间为1s，长木板的位移大小为0.5m．

本题解析：

本题难度：简单

3、简答题  如图5-15所示，甲、乙两小孩各乘一辆冰车在水平冰面上游戏。甲和他的冰车总质量共为30kg，乙和他的冰车总质量也是30kg。游戏时，甲推着一个质量为15kg的箱子和他一起以2m/s的速度滑行，乙以同样大小的速度迎面滑来。为了避免相撞，甲突然将箱子滑冰面推给乙，箱子滑到乙处，乙迅速抓住。若不计冰面摩擦，求甲至少以多大速度（相对地）将箱子推出，才能避免与乙相撞？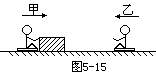

参考答案：v=5.2m/s，方向与甲和箱子初速一致。

本题解析：【错解分析】错解： 设甲与他的冰车以及乙与他的冰车的质量为M，箱子的质量为m，开始时他们的速率为v0，为了不与乙相碰。
　　错解一：甲必须停止，所以，对甲和他的冰车及箱子，推出前后满足动量守恒，由动量守恒定律：
（M+m）v0=0+mv
　　
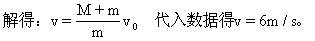
　　错解二：乙接到箱子后停下，所以，对箱子及乙和他的冰车，接到箱子前后动量守恒，设箱子的运动方向为正方向，由动量守恒定律有：
mv－Mv0=0
　　
　　在此题中，有两个关键问题必须弄清楚，第一，“不相撞”的意义，是否意味着一个物体停下，实际上，不相撞的意义就是两个物体的速度相等（同向情况）。物体停止运动，也不一定就撞不上。如本题错解二。按照错解答案我们可知，当甲用4m/s的速度推箱子，箱子以4m/s的速度迎面向乙滑去，与乙相互作用后，乙与箱子都停下来了。那么，此时甲停了吗？我们可以继续完成本题，设甲推出箱子的速度为v"，对甲和箱子，（以甲和箱子的初速度为正），由动量守恒定律有：
（M+m）v0=Mv"+mv
　　解得：v"=1m/s。符号为正，说明甲以4m/s的速度推出箱子后继续向前运动，而乙接住箱子后要停下，这样甲就与乙相撞，所以4m/s的速度太小了。结果不符合题目要求。第二个关键在于不仅要不相撞，而且还要求甲推箱子的速度为最小，即若甲用相当大的速度推箱子，乙接到箱子后还会后退，这样就不满足“至少”多大的条件了，错解一即是这样，将所求的数据代入可以得知，乙和箱子将以0.67m/s的速度后退。
　　【正确解答】 要想刚好避免相撞，要求乙抓住箱子后与甲的速度正好相等，设甲推出箱子后的速度为v1，箱子的速度为v，乙抓住箱子后的速度为v2。
　　对甲和箱子，推箱子前后动量守恒，以初速度方向为正，由动量守恒定律：
（M+m）v0= mv+Mv1①
　　对乙和箱子，抓住箱子前后动量守恒，以箱子初速方向为正，由动量守恒定律有：
mv－Mv0=（m+M）v2②
　　刚好不相撞的条件是：
v1="v" ③
　　联立①②③解得：v=5.2m/s，方向与甲和箱子初速一致。
　　【小结】 本题从动量守恒定律的应用角度看并不难，但需对两个物体的运动关系分析清楚（乙和箱子、甲的运动关系如何，才能不相撞）。这就需要我们要将“不相撞”的实际要求转化为物理条件，即：甲、乙可以同方向运动，但只要乙的速度不小于甲的速度，就不可能相撞。

本题难度：简单

4、计算题  在光滑水平地面上放有一质量为M带光滑弧形槽的小车，一个质量为m的小铁块以速度V0沿水平槽口滑去，如图所示，求：
(1)铁块能滑至弧形槽内的最大高度：(设m不会从左端滑离M)
(2)小车的最大速度；
(3)若M＝m，则铁块从右端脱离小车后将作什么运动？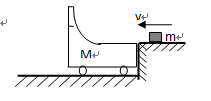

参考答案：（1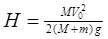）（2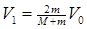）（3）自由落体运动

本题解析：(1)铁块滑至最高处时，有共同速度V，
由动量守恒定律得：mV0＝(M+m)V?　 ①（1分）
由能量守恒定律得：
?　　　②（2分）
由①②解得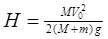：（1分）
(2)铁块从小车右端滑离小车时，小车的速度最大为V１，此时铁块速度为V２，由动量守恒定律得：　　mv＝MV１　+　mV２?　　?③（1分）
由能量守恒定律得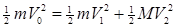：　 　　　　　④（2分）
由③④解得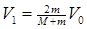：　　（1分）
(3)由上面③④解得:　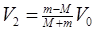　　 ?⑤（1分）
由已知当M＝m时，由⑤得：V2＝０（1分）
又因铁块滑离小车后只受重力，所以做自由落体运动．（1分）

本题难度：一般

5、选择题  关于能量转化与守恒的理解，下列说法中正确的是
A.凡是能量守恒的过程就一定会发生
B.摩擦生热的过程是不可逆过程
C.空调机既能致热又能制冷，说明热传递不存在方向性
D.由于能量的转化过程符合能量守恒定律，所以不会发生能源危机

参考答案：B

本题解析：

本题难度：简单