1、选择题  原来静止在匀强磁场中的原子核A发生衰变后放出的射线粒子和新生成的反冲核都以垂直于磁感线的方向运动，形成如图所示的“8”字型轨迹，已知大圆半径是小圆半径的n倍，且绕大圆轨道运动的质点沿顺时针方向旋转。下列判断正确的是 （?）

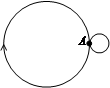
A．该匀强磁场的方向一定是垂直于纸面向里的
B．原子核A的原子序数是2n+2
C．沿小圆运动的是放出的射线粒子，其旋转方向为顺时针
D．沿小圆运动的是反冲核，其旋转方向为逆时针

参考答案：B

本题解析：因为衰变后形成了“8”字型轨迹，这个衰变为a衰变，大圆的轨迹为顺时针，根据洛伦兹力的方向判断出磁场方向垂直纸面向里，A错；由半径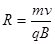，衰变前后动量守恒，生成的新核电荷数为2n,原来的原子核核电荷数为2n+2，B对；衰变前后动量守恒，衰变后动量方向相反，小圆旋转方向为顺时针，CD错；

本题难度：简单

2、简答题  

如图12-1所示，有两块大小不同的圆形薄板(厚度不计)，质量
分别为M和m，半径分别为R和r，两板之间用一根长为0.4m的轻
绳相连结。开始时，两板水平放置并叠合在一起，静止于高度为
0.2m处。然后自由下落到一固定支架C上，支架上有一半径为
R‘(r<R’<R)的圆孔，圆孔与两薄板中心均在圆板中心轴线上，木
板与支架发生没有机械能损失的碰撞。碰撞后，两板即分离，直到
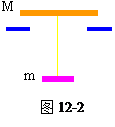
轻绳绷紧。在轻绳绷紧的瞬间，两物体具有共同速度V，如图12-2所示。
求：(1)若M=m，则V值为多大 (2)若M/m=K，试讨论 V的方向与K值间的关系。

参考答案：（1）V=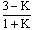
（2）①K＜3时，V＞0，两板速度方向向下。
②K＞3时，V＜0，两板速度方向向上。
③K=3时，V=0，两板瞬时速度为零，接着再自由下落。

本题解析：开始 M与m自由下落，机械能守恒。M与支架C碰撞后，M以原速率返回，向上做匀减速运动。m向下做匀加速运动。在绳绷紧瞬间，内力(绳拉力)很大，可忽略重力，认为在竖直方向上M与m系统动量守恒。(1)据机械能守恒：(M+m)gh=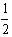(M+m)V02所以，V0=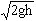=2m/s
M碰撞支架后以Vo返回作竖直上抛运动，m自由下落做匀加速运动。在绳绷紧瞬间，M速度为V1，上升高度为h1，m的速度为V2，下落高度为h2。则：
　　h1+h2=0.4m，h1=V0t-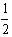gt2，h2=V0t+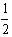gt2，而h1+h2=2V0t，
故：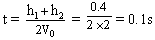
所以：V1=V0-gt="2-10×0.1=1m/s" V2=V0+gt=2+10×0.1=3m/s
根据动量守恒，取向下为正方向，mV2-MV1=(M+m)V，所以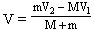
那么当m=M时，V=1m/s；当M/m=K时，V=。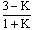
讨论：①K＜3时，V＞0，两板速度方向向下。
②K＞3时，V＜0，两板速度方向向上。
③K=3时，V=0，两板瞬时速度为零，接着再自由下落。

本题难度：简单

3、简答题  

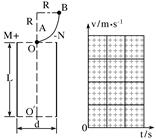
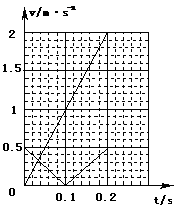
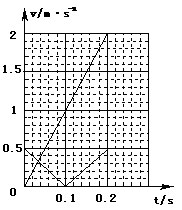
(2)若两小球恰从下边界上的O′点离开电场，则金属板长度L应为多长？并在图示坐标纸上画出两小球在电场中水平方向和竖直方向两个分运动的v-t图象，要求标明坐标值。

参考答案：（1）两小球不能与M板发生碰撞
（2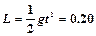）m

本题解析：(1)小球B滑到最低点时的速度为v0，由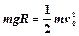? (2分)

得v0=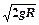="1m/s?" (1分)
两小球碰后的共同速度设为v1，由动量守恒定律得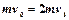? (2分)
解得v1="0.5m/s?" ? (1分)
碰后两小球进入匀强电场，水平方向做匀减速直线运动，竖直方向做自由落体运动
水平方向上加速度大小为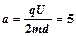：m/s2? (2分)
当水平分速度减为零时，向左运动的位移最大，
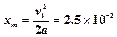m? (2分)
因为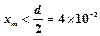m? (1分)
故两小球不能与M板发生碰撞。? (1分)
(2)两小球恰从O′点离开电场，则两小球在电场中运动的时间为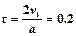s? (1分)
得金属板长度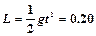m? (2分)
两个分运动的v-t图象如图所示。? (3分)

本题难度：一般

4、计算题  如图所示，以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上滑板.滑板运动到C时被牢固粘连。物块可视为质点，质量为m，滑板质量M=2m，两半圆半径均为R，板长ι=6.5R，板右端到C的距离L在R<L<5R范围内取值，E距A为S=5R，物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5，重力加速度取g.
（1） 求物块滑到B点的速度大小；
（2） 试讨论物块从滑上滑板到离开滑板右端的过程中，克服摩擦力做的功Wf与L的关系，并判断物块能否滑到CD轨道的中点。

参考答案：解：(1)物块从E 点运动到B 点的过程中，只有皮带对物块的摩擦力和重力两个力做功，对该过程应用动能定理得：

(2)物块m和木板M在相互作用的过程中动量守恒，设两者可以达到共同速度，设为V1,该过程中木板运动的位移为X1，两者的相对位移为x。
由动量守恒定律得：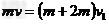
所以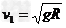
由能量守恒定律得：
对木板应用动能定理得：
当时，到达C点的整个过程中始终存在滑动摩擦力，所以克服摩擦力做功为:
当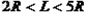时，物块和木板可以达到相同的速度，此后直到木板碰到C点这一过程中，物块和木板之间是没有摩擦力的，该阶段摩擦力不做功。故这种情况下克服摩擦力做功为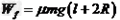：，与L无关。
综合两种情况可知，当L=R时，物块克服摩擦力做功最小，这个过程中物块到达C点的速度最大，对这个过程有：滑上CD轨道后，
设上升的最大高度为h,由机械能守恒定律得：
可见物块滑不到CD轨道的中点。

本题解析：

本题难度：困难

5、选择题  关于牛顿运动定律和动量守恒定律的适用范围，下列说法正 确的是
[? ]
A．牛顿运动定律也适合解决高速运动的问题
B．牛顿运动定律也适合解决微观粒子的运动问题
C．动量守恒定律既适用于低速，也适用于高速运动的问题
D．动量守恒定律适用于宏观物体，不适用于微观粒子

参考答案：C

本题解析：

本题难度：简单