1、选择题  一质量为m的木块，由碗边滑向碗底，碗内表面是半径为r的球面，由于摩擦力的作用，木块运动的速率不变，则
A.木块的加速度为零
B.木块所受合外力为零
C.木块所受合外力的大小一定，方向改变
D.木块的加速度大小不变

参考答案：CD

本题解析：木块做匀速圆周运动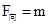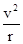，合力指圆心，加速度不为零，所以A错；B错；合力就是向心力，时刻指向圆心，方向时刻改变，C正确，加速度的大小不变，方向时刻改变，D正确，故答案选CD。
思路分析：解决本题应当掌握匀速圆周运动受力特点：做匀速圆周运动的物体合外力提供向心力，其向心力大小不变，方向始终指向圆心
试题点评： 本题很简单，考察了匀速圆周运动向心力特点，注意向心力是根据效果命名的，只能由其它力充当

本题难度：一般

2、选择题  质量为m的小球在竖直平面内的圆形轨道的内侧运动，经过最高点而不脱离轨道的速度临界值是v．当小球以3v?的速度经过最高点时，对轨道的压力值是（　　）
A．3?mg
B．8?mg
C．9?mg
D．10?mg

参考答案：当小球以速度v经内轨道最高点时，小球仅受重力，重力充当向心力，有mg=mv2r
当小球以速度3v经内轨道最高点时，小球受重力G和向下的支持力N，如图，合力充当向心力，有mg+N=m(3v)2r；



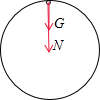
又由牛顿第三定律得到，小球对轨道的压力与轨道对小球的支持力相等，N′=N；
由以上三式得到，N′=8mg；
故选B；

本题解析：

本题难度：一般

3、简答题  如图所示，位于竖直面内的曲线轨道的最低点B的切线沿水平方向，且与一位于同一竖直面内、半径R=0.40m的光滑圆形轨道平滑连接．现有一质量m=0.10kg的滑块（可视为质点），从位于轨道上的A点由静止开始滑下，滑块经B点后恰好能通过圆形轨道的最高点C．已知A点到B点的高度h=1.5m，重力加速度g=10m/s2，空气阻力可忽略不计，求：
（1）滑块通过C点时的速度大小；
（2）滑块通过圆形轨道B点时对轨道的压力大小；
（3）滑块从A点滑至B点的过程中，克服摩擦阻力所做的功．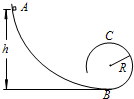

参考答案：解；（1）因滑块恰能通过C点，即在C点滑块所受轨道的压力为零，其只受到重力的作用．
设滑块在C点的速度大小为vC，根据牛顿第二定律，对滑块在C点有
mg=mvc2R
解得vC=

本题解析：

本题难度：一般

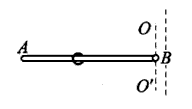
4、计算题  如图所示，水平长杆AB绕过B端的竖直轴OO"匀速转动，在杆上套有一个质量m=1kg的圆环，若圆环与水 平杆间的动摩擦因数μ=0.5，且假设最大静摩擦力与滑动摩擦力大小相等，则：
(1)当杆的转动角速度ω=2 rad/s时，圆环的最大回转半径为多大？
(2)如果水平杆的转动角速度降为ω"=1.5 rad/s，圆环能否相对于杆静止在原位置，此时它所受到的摩擦力有多大？(g 取10 m/s2）

参考答案：解：
(1)圆环在水平面内做匀速圆周运动的向心力是杆施加给它的摩擦力提供的，则最大向心力F向=μmg，代入公式F向= mRmaxω2，得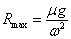．代入数据可得Rmax=1.25 m．
(2)当水平杆的转动角速度降为1.5 rad/s时，圆环所需的向心力减小，则圆环所受的静摩擦力随之减小，不会相对于杆滑动，故圆环相对杆仍静止在原来的位置，此时的静摩擦力f= mRmaxω"2=2.81 N．

本题解析：

本题难度：一般

5、选择题  在世界一级方程式锦标赛中，赛车在水平路面上转弯时，常常在弯道上冲出跑道，则以下的说法正确的是（　　）
A．是由于赛车行驶到弯道时，运动员未能及时转动方向盘才造成赛车冲出跑道的
B．是由于赛车行驶到弯道时，没有及时加速才造成赛车冲出跑道的
C．是由于赛车行驶到弯道时，没有及时减速才造成赛车冲出跑道的
D．由公式Fm=mω2r可知，弯道半径越大，越容易冲出跑道

参考答案：赛车行驶到弯道时，由于速度过大，使赛车受到的静摩擦力不足以提供所需的向心力，所以赛车将沿切线方向冲出跑道．选项C符合题意．
故选：C．

本题解析：

本题难度：简单